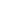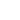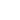1.2.1 Приложение
Вычислим интеграл от произвольной функции
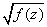 на отрезке от
на отрезке от
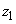 до
до
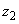 .
.
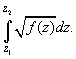
(П1)
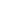
Определим величину
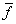 как
как
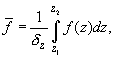
(П2)
то есть
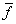 – среднее значение функции
– среднее значение функции
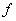 на отрезке от
на отрезке от
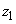 до
до
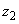 ,
,
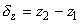 . Тогда уравнение (П1) можно переписать в виде
. Тогда уравнение (П1) можно переписать в виде
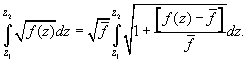
(П3)
Раскладывая подынтегральное выражение (П3) в ряд Тейлора и пренебрегая членами
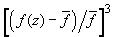 более высшего порядка, получим
более высшего порядка, получим
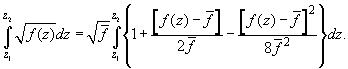
(П4)
Второй член в (П4) при интегрирование равен нулю, поэтому выражение (П4) можно записать в виде
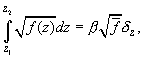
(П5)
где поправочный коэффициент
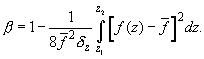
(П6)