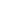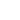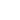1.2.2 Формула John G. Simmons в случае малого, промежуточного и высокого напряжения

В пункте 1.2.1 показано, что туннельный ток, протекающий в системе металл-диэлектрик-металл (М-Д-М), выражается общей формулой [1]:

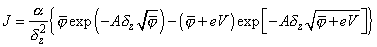
(1)

где 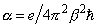, , 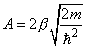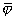– среднее значение потенциального барьера, 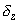– ширина потенциального барьера, 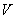– напряжение между металлами.

При низких напряжениях 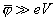, выражение (1) можно привести к более простому виду [1]

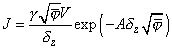
(2)

где 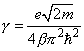. Так как 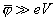, то можно считать, что 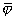не зависит от 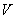. Таким образом, в случае малого значения прикладываемого напряжения, туннельный ток линейно зависит от 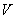. Энергетическая диаграмма системы М-Д-М когда 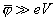представлена на рис. 1.

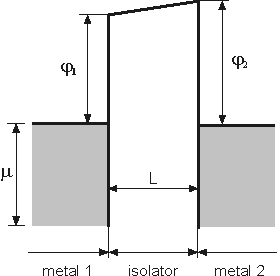
Рис. 1. Потенциальный барьер в системе М-Д-М в случае 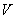~ 0.
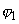и 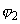– работы выхода металлов соответственно.

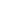
Если 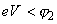, тогда 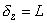и 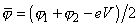(рис. 2).

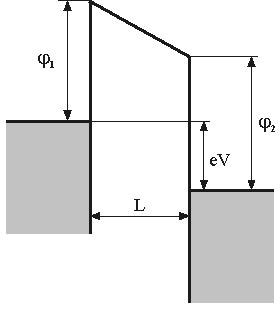
Рис. 2. Потенциальный барьер в системе М-Д-М в случае .
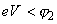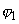и 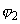– работы выхода металлов соответственно.

В [2] показано, что в этом случае зависимость туннельного тока от напряжения

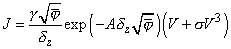
(3)

где .

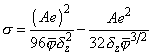Высокое напряжение – Автоэмиссионный режим.

Случаю, когда 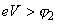соответствует энергетическая диаграмма, изображённая на рис. 3 и , .

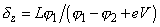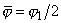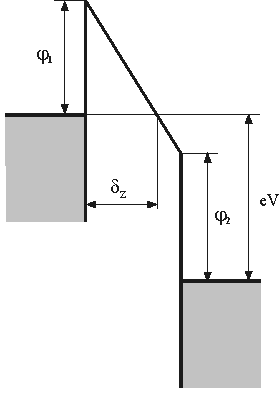
Рис. 3. Потенциальный барьер в системе М-Д-М в случае .
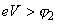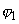и 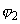– работы выхода металлов соответственно.

Подставляя эти значения 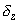и 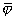в уравнение (1), имеем

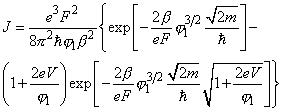
(4)

где 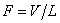– напряжённость электрического поля.

При очень высоких напряжениях ( 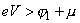) уровень Ферми 2-ого электрода лежит ниже дна зоны проводимости 1-ого электрода. Поэтому при таких условиях, электроны не могут туннелировать из 2-ого в 1-ый электрод, так как нет свободных уровней. Совершенно обратная ситуация наблюдается для противоположного направления туннелирования, так как для электронов 1-ого электрода становятся доступны все свободные уровни 2-ого электрода. Такая ситуация аналогична явлению холодной эмиссии электронов из металла в вакуум. Таким образом, так как 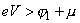, то вторым слагаемым в (4) можно пренебречь и соответственно

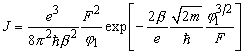
(5)

где b = 23/24. Полученный результат качественно совпадает с аналитическим выражением для плотности токa автоэлектронной эмиссии [3].

Таким образом, с помощью формул (1)–(5) можно теоретически рассчитать величину туннельного тока при заданных параметрах системы и соответственно построить вольтамперные характеристики. На рис. 4 представлена теоретическая зависимость туннельного тока от прикладываемого напряжения в случае углеродного электрода 1 (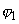 = 4,7 эВ) и платинового электрода 2 (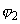 = 5,3 эВ) при 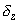= 5 Å и контактной площади S = 10^-17 m².

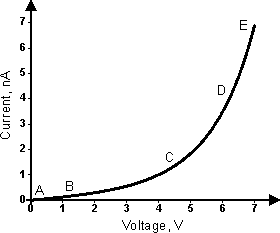
Рис. 4. Вольтамперная характеристика в случае углеродного электрода 1 и платинового электрода 2 при 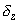= 5 Å и контактной площади 10^-17 m². Обозначенные участки кривой J(V) зависят от V по соответствующим формулам: AB – (22), BC – (23), CD – (24), DE – (25).

Выводы.

В зависимости от величины напряжения, прикладываемого к системе М-Д-М, формулу John G. Simmons можно преобразовать к более упрощённым вариантам (2)–(5).
Экспериментальные зависимости туннельного тока от параметров задачи, можно описывать приближёнными зависимостями (2)–(5) в соответствии с величиной прикладываемого напряжения.

Литература.

John G. Simmons. J. Appl. Phys. - 1963. - V. 34 1793.
John G. Simmons. J. Appl. Phys. - 1963. - V. 34 238.
Л.Н. Добрецов, М.В. Гомоюнова. Эмиссионная электрони-ка // М.: Наука, 1966.