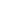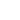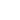2.7.12 Магнитное поле периодических параллельных доменов

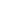
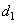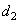Вычислим, внешнее магнитное поле, создаваемое периодической структурой параллельных доменов шириной и , намагниченность 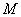которых одинакова по модулю, но чередуется по направлению от домена к домену (рис. 1).

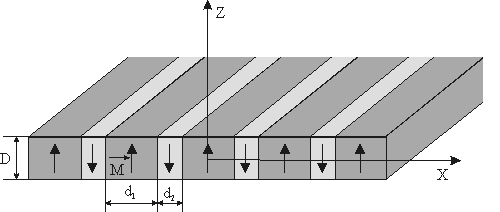
Рис. 1. Схематическое изображение периодической параллельной структуры магнитных доменов.

Будем рассматривать только случай, когда вектор намагниченности 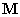направлен перпендикулярно к поверхности образца, как показано на рис. 1. Так же считаем, что толщина магнитной плёнки 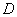постоянна по всей поверхности образца, а её длина и ширина бесконечны.

Данная задача рассматривалась в работе [1] и полученные результаты будут приведены здесь без выводов. Магнитостатическая энергия структуры, изображённой на рис. 1, согласно [1] запишется в виде

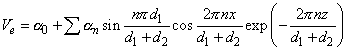
(1)

где

(2)

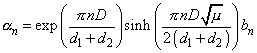
(3)

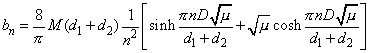
(4)

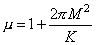
(5)

и 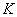– константа анизотропии энергии кристалла. Внешнее магнитное поле 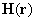создаваемое данной структурой запишется в виде:

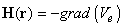
(6)

Таким образом, подставляя выражение (1) в (6) найдём искомое магнитное поле в любой точке пространства над образцом.

В МСМ обычно измеряется вторая производная магнитного поля по координате вдоль направления колебаний зонда (см. пункт 2.7.1). Поэтому, для определения качественной зависимости изменения регистрируемых параметров в МСМ необходимо проанализировать качественное изменение величины 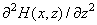в зависимости от соотношения между входящими параметрами задачи. На рис. 2–4 показано изменение величины 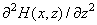вдоль оси 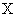вычисленное в соответствие с формулами (1)–(6), при заданном значении координаты 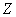, , 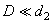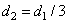и различных соотношениях между 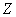и .

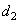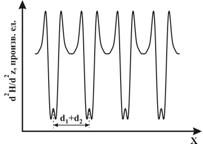
Рис. 2. Качественная зависимость 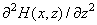вдоль оси 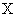на высоте .

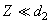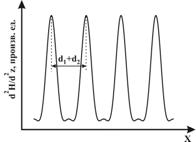
Рис. 3. Качественная зависимость 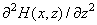вдоль оси 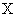на высоте .

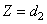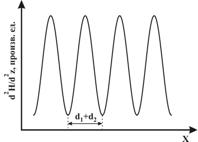
Рис. 4. Качественная зависимость 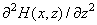вдоль оси 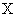на высоте .

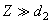Как видно из рисунков 2–4, исследуемые зависимости имеют период равный 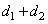и качественно отличаются при различных значениях .

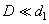Качественная зависимость 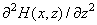от расстояния 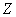в фиксированной точке 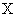(на границе между доменами) при условии 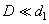, 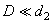представлена на рис. 5.

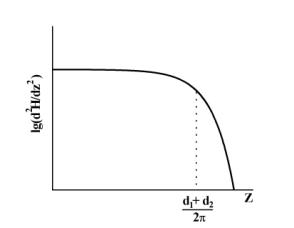
Рис. 5. Качественная зависимость 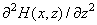вдоль оси .

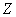В этом случае, магнитное поле, так же как и для цилиндрического домена (пункт 2.7.11), спадает на расстояниях определяемых геометрическими размерами магнитной структуры.

Таким образом, если при качественном исследовании распределения магнитного поля в режиме сканирования было обнаружено, что магнитные домены имеют ламинарную структуру (рис. 1), то сравнение профилей изменения фазы вдоль строки сканирования 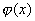с результатами, приведенными на рис. 2–5, позволяет сделать вывод о соотношении размеров доменов и толщины магнитной пленки. Количественный анализ возможен, если подобрать единственный набор параметров 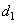, 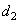и 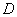так, чтобы результаты расчета по формулам (1–6) наиболее точно удовлетворили экспериментальным профилям 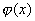. Для этой цели возможно использовать специально разработанную Flash модель, которая теоретически рассчитывает изменение амплитуды, фазы или резонасной частоты колебаний зонда во втором проходе стандартного динамического МСМ режима.

Выводы.

Вычислено магнитное поле (1)–(6), создаваемое периодической (ламинарной) структурой параллельных доменов ширино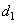й и 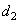, намагниченность 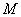которых одинакова по модулю, но чередуется по направлению от домена к домену.
В случае, если при качественном исследовании распределения магнитного поля в режиме сканирования обнаружено, что магнитные домены имеют ламинарную структуру, то сравнение профилей изменения фазы вдоль строки сканирования 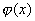с результатами, приведенными на рис. 2–5, позволит определить соотношение размеров доменов и толщины магнитной пленки.
Количественный анализ возможен, если подобрать единственный набор параметров 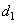, 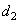и 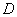так, чтобы результаты расчета по формулам (1–6) наиболее точно удовлетворили экспериментальным профилям .

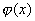Литература.

С. Kooy, U. Enz, Philips Res. Repts. 15, 7-29, (1960)