1.1.3 Зонная структура металлов, энергетическое распределение электронов в металле

Для вывода формулы туннельного тока в системе металл-диэлектрик-металл (формула John G. Simmons, см. пункт 1.2.1), необходимо ввести ряд упрощающих положений и напомнить некоторые основы электронной теории металлов.

Во-первых, будем считать, что всё твёрдое тело (металл) представляется как трехмерная потенциальная яма с гладким дном (так называемая модель Зоммерфельда) и электроны между собой не взаимодействуют. Энергия электрона, покоящегося на дне такой ямы, меньше, чем уровень вакуума – энергия покоящегося электрона, находящегося на бесконечности от поверхности тела. Глубина потенциальной ямы U определяется усреднённым полем положительных ионов решётки и всех электронов.
Во-вторых, так как все электроны считаются невзаимодействующими, то решение уравнения Шредингера для системы электронов сведется к решению уравнения Шредингера для одного электрона, движущегося в этом усреднённом поле, что позволяет использовать формулы (3) пункта 1.1.1 или (4) in пункта 1.1.2.
В третьих, в потенциальном ящике с гладким дном зависимость разрешённых значений энергии от разрешённых значений волнового вектора оказывается точками на параболической зависимости энергии от компонент волнового вектора 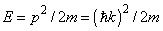для свободного электрона в пустом пространстве. Если масса электронов m изотропна во всём пространстве, то справедливо 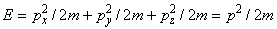, где 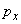, , 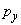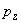– импульсы электрона вдоль соответствующих осей.

Из статистической физики [1] известно, что в системе, находящейся в термодинамическом равновесии с температурой T, все квантовые состояния с одним и тем же значением энергии E заполнены электронами одинаково. Среднее число электронов находящихся в одном квантовом состоянии с энергией E при температуре T определяется распределением Ферми-Дирака:

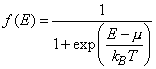
(1)

где 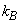= (11600)^–1 eV/К – постоянная Больцмана, 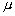– параметр, имеющий размерность энергии и называемый химическим потенциалом.

Химический потенциал 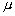определяется из условия нормировки

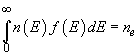
(2)

где n_e – число электронов зоны проводимости на единицу объема (концентрация), 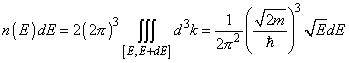– число электронных состояний на единицу объема в интервале энергий от E до E + dE. n(E) называется энергетической плотностью числа состояний.

В металле при температуре, стремящейся к абсолютному нулю, электроны заполняют все квантовые состояния с энергиями вплоть до уровня 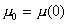называемого уровнем Ферми. Все квантовые состояния с энергией выше уровня Ферми свободны от электронов. Для металла химический потенциал слабо зависит от температуры, поэтому его можно заменить значением 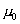при T = 0:

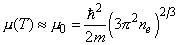
(3)

где m – масса электрона. Если n_e измеряется в системе единиц СГС, тогда .

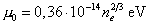Если система находится в тепловом равновесии и состоит из нескольких подсистем, то уровни Ферми, для каждой подсистемы должны совпадать (рис. 1). Если же между двумя подсистемами (телами) приложено напряжение V, то уровень Ферми тела, связанного с плюсом источника напряжения, понижается, а другого тела – повышается. При этом уровни Ферми первого и второго тела отличаются на величину eV (рис. 2).

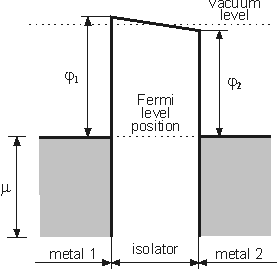
Рис. 1. Модель потенциального барьера МДМ для случая, когда система находится в термодинамическом равновесии;
j₁ и j₂ – работы выхода левого и правого металла соответственно.

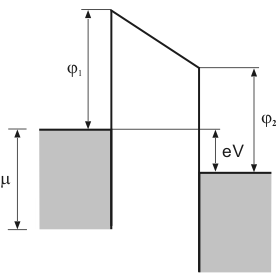
Рис. 2. Модель потенциального барьера МДМ для случая, когда положительный потенциал приложен к правому металлу. Разность потенциалов V.

Выводы.

При решении задачи о туннелировании электронов в системе металл-диэлектрик-металл (пункт 1.2.1) будем считать, что:

Справедлива модель Зоммерфельда.
Каждый электрон в твёрдом теле движется в усреднённом поле других электронов и ионов кристаллической решётки.
Справедлив квадратичный изотропный закон дисперсии для свободного электрона в пустом пространстве.
В металлах при 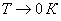, все квантовые состояния с энергиями вплоть до уровня Ферми, вычисляемого по формуле (3), заняты электронами, а все квантовые состояния с энергией выше уровня Ферми свободны.

Литература.

Л.Д. Ландау, Е.М. Лифшиц. Статистическая физика // М.: Наука, 1976.
Ч. Киттель. Введение в физику твёрдого тела // М.: Наука, 1978.