Расширение возможностей атомно-силовой микроскопии с помощью прыжковой АСМ
Пример применений 087(pdf 6.3 Mb)
- Углубленная детализация изображений наноразмерных структур - одна из замечательных особенностей Прыжковой АСМ (HybriD Mode)
- Отображение локальной адгезии и жесткости с высоким разрешением в Прыжковой АСМ расширяет возможности картирования состава гетерогенных материалов и превращает АСМ в инструмент количественного анализа локальных механических свойств
- Сочетание прыжковой АСМ с многомодовыми резонансными методиками дает основу для всесторонней характеризации материалов на наноуровне
Сергей Магонов, NT-MDT Development Inc.
Спектр методов атомно-силовой микроскопии (АСМ) в последнее время пополнился прыжковой АСМ (П-АСМ) которая позволяет регистрировать изгибы кантилевера в процессе колебательного взаимодействия между зондом и образцом с высокой точностью. Реализация П-АСМ стала возможной благодаря разработке быстродействующих систем сбора данных и обработки сигналов в режиме реального времени. Он открывает новые перспективы в применении АСМ. Регистрация сигнала изгиба в течение всего цикла взаимодействия позволяет по-новому организовать управление с помощью обратной связи и произвести картирование механических и электромагнитных свойств образца.
Экспериментальные данные, полученные с помощью П-АСМ для ряда образцов, демонстрируют её уникальные возможности. На их основе можно выявить преимущества П-АСМ по сравнению с амплитудно-модуляционной АСМ (АМ-АСМ), которая к настоящему времени получила довольно широкое распространение.
ВВЕДЕНИЕ
Атомно-силовая микроскопия является эффективным инструментом визуализации поверхности с высоким разрешением и исследования локальных свойств материалов этой поверхности. Силовое взаимодействие между кончиком миниатюрного зондового датчика и поверхностью образца сосредоточено в области с размерами порядка нескольких нанометров, и поэтому регистрация этого взаимодействия дает уникальные по чувствительности и пространственному разрешению данные об образце. В настоящее время АСМ включает широкий спектр методов, которые постоянно совершенствуются путем повышения чувствительности детекторов силового взаимодействия и быстродействия электронных схем регистрации, а также благодаря внедрению многочастотных измерений в широком спектре частот.
Наличие большого выбора методов АСМ измерений позволяет получать профили поверхности с высоким разрешением, визуализировать поверхностные структуры и исследовать их механические и электромагнитные свойства.
Однако оптимальный выбор подходящего метода и условий измерений, обеспечивающего наилучшие данные об интересующем свойстве или структуре образца, может оказаться весьма непростым. Ниже будет рассмотрена П-АСМ, использующая колебания на нерезонансной частоте кантилевера, в которой применяется прерывистый контакт между зондом и образцом, влияние которого на изгиб кантилевера используется для обратной связи в процессе сканирования поверхности. Анализ возможностей П-АСМ будет проведен на основе сравнения её результатов с результатами АМ-АСМ [1, 2], в которой зонд осциллирует на резонансной частоте, а изображение поверхности строится по сигналу, обусловленному изменением амплитуды колебаний.
Идея снижения влияния латерального взаимодействия между зондом и образцом путем использования прерывистого контакта была впервые реализована в профилометре с осциллирующим зондом в 1955 г. [3], а для АСМ эта концепция была сформулирована в 1989 г. в виде метода «jumping mode», для которого были предложены схемы аналогового и цифрового управления прибором [4]. В ряде других колебательных методик, включая АМ-АСМ, зонд или генератор работают на резонансной частоте, что позволяет повысить чувствительность измерений. Сложность использования этих методов заключается в необходимости разработки корректной количественной интерпретации откликов по амплитуде, фазе и частоте колебаний для получения информации о локальных свойствах материалов. В П‑АСМ образец и зонд взаимодействуют на частоте ниже резонансов пьезопривода и кантилевера, что упрощает анализ взаимодействия между образцом и зондом.
Это обстоятельство позволяет сканировать поверхность при постоянном изгибе кантилевера аналогично контактному методу и при этом меньше воздействовать на образец благодаря снижению латеральных сил. Помимо этого, в методе П-АСМ регистрируется сигнал отклонения зонда на протяжении всего цикла осцилляций, по которому можно получить информацию о различных силах взаимодействия между зондом и образцом (дальнодействующих, адгезионных и контактных) и затем построить распределения этих сил наряду с рельефом образца.
Основные методические и аппаратные особенности реализации этого метода в приборах НТ-МДТ Спектрум Инструментс будут описаны ниже. Эффективность этой реализации будет продемонстрирована на примерах данных, полученных для различных образцов. Надежность картирования адгезионных сил и жесткости подтверждается данными для бинарных материалов. Сравнение результатов, полученных с применением П-АСМ и АМ-АСМ, показывает, что сочетание П-АСМ и с многочастотными методами АМ-АСМ дает основу для наиболее детальных исследований с помощью АСМ.
АППАРАТНЫЕ ОСОБЕННОСТИ
Компания НТ-МДТ Спектрум Инструментс разработала новый электронный контроллер, применение которого повысило исследовательский потенциал микроскопов за счет реализации высокочувствительных режимов АСМ, реализованных путем снижения флуктуаций отклонений (~25 фм/√Гц) и управляющего высокого напряжения (шум < 1 мВ/600 В) и внедрения многочастотных методик на основе пяти синхронных детекторов.
Эти усовершенствования позволили получить изображения с атомным разрешением кристаллических образцов кальцита и tetrathiafulvalene - tetracyanoquinodimethane с использованием АМ-АСМ метода [5] и реализовать однопроходное картирование поверхностного потенциала с нанометровым разрешением [6], а также многочастотные измерения пьезоотклика [7]. К контроллеру добавлен модуль высокоскоростного (20 МГц) получения данных, с помощью которого в микроскопах НЕКСТ и ИНТЕГРА стала возможной регистрация отклонений зонда в реальном времени для диапазона 0.5 - 10 кГц в ходе цикла измерений. Модуль обеспечивает обработку поступающих данных с частотой 120 МГц, которая необходима для режима реального времени. Для поддержки новых функций были разработаны новые программные модули программы управления Nova.
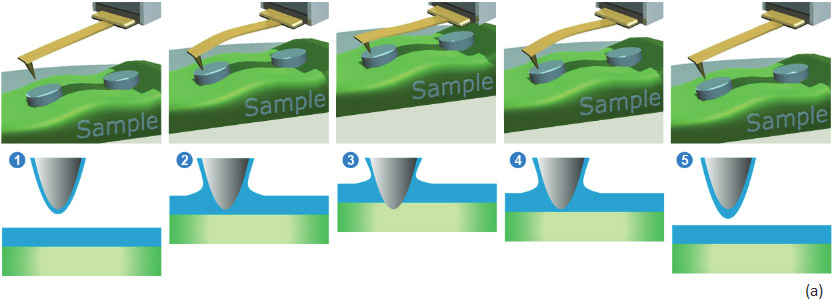
В П-АСМ образец или зондовый датчик приводится в колебания в вертикальном направлении с помощью Z пьезоэлемента, который возбуждается на частоте много ниже резонансных частот зонда и пьезоэлемента. Метод П-АСМ с низкочастотными колебаниями образца реализован в приборах НЕКСТ II, ИНТЕГРА, ИНТЕГРА Нано ИК, ИНТЕГРА Спектра II, СОЛВЕР Опен, НАНОЭДЬЮКАТОР II, СОЛВЕР Нано. В приборах ВЕГА, СОЛВЕР Пайп II, СМЕНА применяются низкочастотные колебания АСМ зондом, закрепленным на пьезосканере. В ходе сближения зонда и образца в отдельном цикле измерений зонд вступает в контакт с образцом, а кантилевер дополнительно отклоняется в соответствии с уровнем взаимодействия между зондом и образцом, заданным оператором.
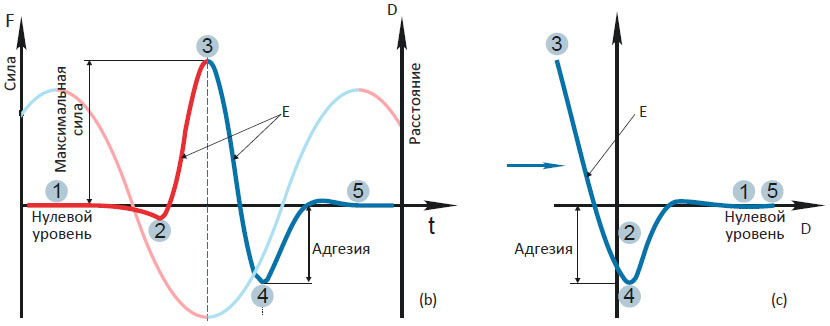
Основные этапы цикла измерений в П-АСМ для идеализированной характеристики отклонений зонда показаны на Рис. 1a-b. В начале сближения зонда и образца изгиб кантилевера остается постоянным на базовом уровне (точка 1 на профиле отклонений), а затем под действием адгезионных и капиллярных сил кантилевер изгибается вниз (точка 2).
При дальнейшем сближении начинают преобладать силы отталкивания, которые вынуждают кантилевер изогнуться вверх до уровня (точка 3), заданного для обратной связи в ходе латерального сканирования. Далее направление движения по координате Z изменяется на противоположное. На траектории удаления зонда от образца может оказаться участок сильного адгезионного притяжения, которому соответствует потенциальная яма (точка 4) на профиле изгибов, после которого взаимодействие зонда с образцом пропадает, и изгиб кантилевера возвращается на базовый уровень (точка 5).
Кривые временной зависимости изгибов кантилевера содержат большое количество полезной информации, которая может быть зарегистрирована и отображена в ходе сканирования поверхности, а затем использована для количественной характеризации локальных свойств образца.
Например, на значение базового уровня могут влиять дальнодействующие электростатические и магнитные силы, к которым чувствительны зонды с проводящими и ферромагнитными покрытиями, соответственно. Проводящие зонды позволяют регистрировать также ток между зондом и образцом или локальный пьезоотклик в течение этапов цикла измерений, в которых зонд касается образца.
Для измерения адгезионных сил можно использовать характеристики потенциальной ямы на кривых подвода-отвода. Наклон кривой подвода-отвода в области контакта между зондом и образцом связан с жесткостью образца. Выбор рабочей точки для изгиба зависит от цели эксперимента. При низких значениях рабочей точки мало воздействие на образец, а при высоких можно проводить картирование наномеханических свойств.
Рассмотренные особенности временных зависимостей изгиба кантилевера и связанных с ними кривых зависимости изгиба от расстояния Z (DvZ) (Рис. 1c) хорошо известны и давно используются для анализа данных контактных методов [8, 9]. Кривые DvZ (или силовые кривые) в контактных методах регистрируются на частотах в ограниченном диапазоне частот от 0.1 до 10 Гц, что существенно сужает их применение. С появлением П-АСМ этот недостаток устраняется: данные регистрируется в режиме реального времени, анализ и отображение полученных данных производятся на частотах порядка нескольких кГц.
Параллельно с регистрацией основных сигналов в режиме реального времени производится измерение изгибов и их обработка в ходе отдельного цикла измерений. Обычно в микроскопах ИНТЕГРА и НЕКСТ образец колеблется с частотой 1.5 кГц (длительность цикла - 0.67 мс) и амплитудой 50-100 нм, а рабочая точка зонда задается в диапазоне 1-20 нм. Эти настройки соответствуют уровню сил отталкивания 0.2 - 20 нН для кантилевера, имеющего длину 60-300 мкм и жесткость 0.5 ‑ 2 Н/м.
Примеры применений П-АСМ проиллюстрированы на Рис. 2. На Рис. 2a-c показаны изображения высоты рельефа, адгезионным силам и жесткости, полученные от слоя poly(diethyl siloxane) (PDES) на подложке Si. На Рис. 2d-e показаны изображения этого же образца, полученные с применением АМ-АСМ, по которым можно сравнить эффективность П-АСМ и АМ-АСМ. Этот пленка мезоморфного полимера, полученная втиранием в подложку Si, состоит из жестких ламеллярных агрегатов, внедренных в более мягкую аморфную матрицу. Морфология образцов PDES ранее изучалась с помощью метода АМ [10-11].



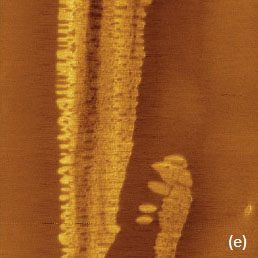
Обычно ламеллярные агрегаты хорошо видны на АМ изображениях. Наилучшее разрешение достигается в методе регистрации фазы (Рис. 2e), который преимущественно используется для картирования неоднородных полимеров по составу [12]. В отличие от изображения высоты рельефа (Рис. 2d), контраст фазового изображения позволяет выявить различные компоненты полимера. К сожалению, интерпретация фазового изображения с целью получения механических свойств образца пока не создана.
Однако для этой цели можно использовать данные П-АСМ - распределения адгезионных сил и жесткости образца, показанные на Рис. 2b,c. На этих картах сильная адгезия наблюдается в аморфных окрестностях ламеллярных агрегатов, а более высокая жесткость - в областях этих агрегатов. Таким образом, П-АСМ позволяет получить независимые распределения адгезионных сил и жесткости, которые в последующем можно использовать для количественного анализа работы адгезии и модуля упругости материала образца. Заметим также, что в отличие от метода АМ на изображении высоты рельефа, полученного с помощью П-АСМ, ламеллярные агрегаты видны. Этот факт ставит вопрос о различии уровней силового взаимодействия между зондом и образцом, применяемых в этих методах, к которому мы вернемся ниже. На Рис. 3 представлены примеры изучения локальных электромагнитных свойств материалов с помощью П-АСМ. На Рис. 3a-d показаны АСМ изображения структур углеродных нанотрубок, нанесенных на подложку Si. Наряду с изображениями по высоте, адгезионным силам и жесткости, в этом случае были измерены данные по току между зондом и образцом. Контраст по локальной адгезии и жесткости позволяет различить нанотрубки и подложку - жесткость нанотрубок ниже, чем у подложки. Данные, представленные на Рис. 3d, показывают, что не на всех участках нанотрубок протекает ток между зондом и образцом, что, по-видимому, объясняется различиями в электронных свойствах этих объектов - среди них могут быть как проводники, так и полупроводники.




Измерения тока проводились только на этапах контакта зонда и образца всех циклов измерений. При переходе к бесконтактным этапам вклад механического взаимодействия между зондом и образцом пренебрежимо мал, а отклонение кантилевера определяется, главным образом, дальнодействующими электростатическими и магнитными силами. Изменение распределения контраста при изменении базового уровня позволяет выявить магнитную структуру образца, в то время как изображение по высоте, которое снимается в фиксированной рабочей точке по отклонению на этапе контакта, дает шероховатость поверхности (Рис. 4a‑b).





О чувствительности П-АСМ изображений по электростатической силе к значению базового уровня можно судить по изображениям углеродных нанотрубок, показанным на Рис. 4c-e. В этом случае при повышении напряжения смещения между проводящим зондом и образцом контраст усиливается.
Контраст отдельной нанотрубки определяется значением притягивающей электростатической силы, который зависит, в основном, от разности локальных поверхностных потенциалов.На практике временные зависимости отклонения от расстояния зачастую имеют более сложную форму, чем рассмотренная выше идеализированная кривая, что объясняется рядом причин. Если образец помещен во внешнюю среду, на поверхностях образца и зонда могут образовываться адсорбаты.
В этих областях для отрыва зонда может потребоваться увеличение амплитуды колебаний. В случае использования мягкого зонда преодоление адгезионных сил может привести к возбуждению резонансных колебаний зонда на одной из собственных частот. Подобное поведение зонда («реверберация») показано на Рис. 5a. Если среда между зондом и поверхностью образца имеет большую плотность (например, жидкость), она будет передавать перемещение образца на кантилевер зонда, что приведет к периодическому отклонению кантилевера вблизи от образца и соответствующему вкладу в виде осциллирующей огибающей на кривой отклонения (Рис. 5b).
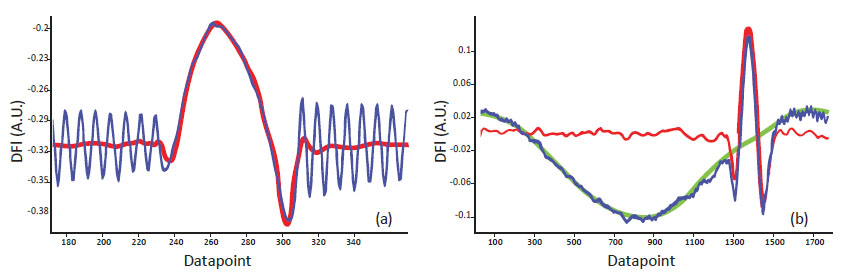
Искажения данных, обусловленные указанными двумя причинами, должны быть устранены в режиме реального времени до того, как начнется обработка кривых отклонения.
Для этой цели регистрируемый сигнал отклонения можно обработать с помощью дискретного вейвлетного преобразования (discrete wavelet transform, DWT). В этой процедуре производится фильтрация входного сигнала с помощью базовых вейвлетов и сжатие выходных данных, повышающее эффективность вычислений по времени. Выбор преобразования DWT обусловлен необходимость проведения частотно-временного анализа сигнала отклонения.
На Рис. 5a показан результат применения фильтрации для устранения реверберации с помощью вейвлета Добеши порядка 3, имеющего 4 нулевых момента. Эти параметры вейвлета установлены в программе управления по умолчанию, однако их можно выбрать по усмотрению пользователя. Применение вейвлета Добеши порядка 8 с 4 нулевыми моментами позволяет полностью очистить сигнал от осциллирующей компоненты (Рис. 5b). П-АСМ в сочетании с фильтрацией в режиме реального времени обеспечивает получение интерпретируемых данных для широкого спектра образцов.
СИЛЫ ВЗАИМОДЕЙСТВИЯ МЕЖДУ ЗОНДОМ И ОБРАЗЦОМ В АМ-АСМ И П-АСМ
Силы взаимодействия между зондом и образцом лежат в основе всех методов АСМ. Контроль над этими силами определяет разрешение изображений поверхности образца и точность измерения локальных свойств. Для предотвращения разрушения образца и получения топографии поверхности с высоким разрешением необходимо проводить измерения при низком уровне взаимодействия между зондом и образцом.
Исследование локальных механических свойств требует определенного силового воздействия на образец, чтобы можно было измерить зависимость между силой и деформацией, по которой можно получить упругие, вязкоупругие или пластические характеристики материала и провести количественный анализ механических свойств.
В методах АСМ значение силы взаимодействия между зондом и образцом зависит, в основном, от чувствительности используемого зонда, уровня рабочей точки, необходимой для работы системы обратной связи, жесткости зонда и размеров кончика зонда. Отклонение кантилевера пропорционально суммарной силе, действующей на образец, которая дается суперпозицией сил притяжения и отталкивания. Сигнал отклонения используется для обратной связи в контактных методах и в П-АСМ.
Поэтому для получения изображений по контрасту силы необходим надлежащий выбор уровня рабочей точки. Зонды, обычно используемые в наших приборах при измерениях с помощью П-АСМ, имеют жесткость в диапазоне от 0.4 Н/мкм до 40 Н/мкм. Для измерений во внешней среде рабочая точка задается на уровне много ниже 1 нм, и поэтому силы взаимодействия между зондом и образцом в этом случае составляют несколько десятков пН.
Оценка сил взаимодействия между зондом и образцом для АМ-АСМ, в котором обратная связь осуществляется по затуханию амплитуды колебаний зонда на частоте первой моды колебаний, невозможна без глубокого теоретического анализа.
Однако общие особенности связи между силой воздействия и деформацией образца в зависимости от амплитуды свободных колебаний зонда A0 и уровня рабочей точки Asp для АМ-АСМ можно получить по результатам численного моделирования процесса взаимодействия по упрощенной модели Герца [13, 14]. В этом случае учитываются только консервативные силы, и соотношение между амплитудами A0 и Asp и фазой колебаний зонда дается уравнениями (1).
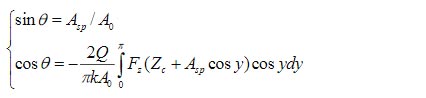 (1)
(1)
где A0 – амплитуда свободных колебаний, Asp – амплитуда рабочей точки; Zc – центральное положение сферы, описывающей форму кончика зонда, относительно поверхности в процессе колебаний, k - упругая постоянная и Q – добротность зондового датчика на первой изгибной моде, Fz – сила воздействия на зонд на этапах подвода и отвода отдельного цикла измерений. Комбинируя эти уравнения, можно получить следующее выражение (2).
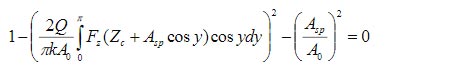 (2)
(2)
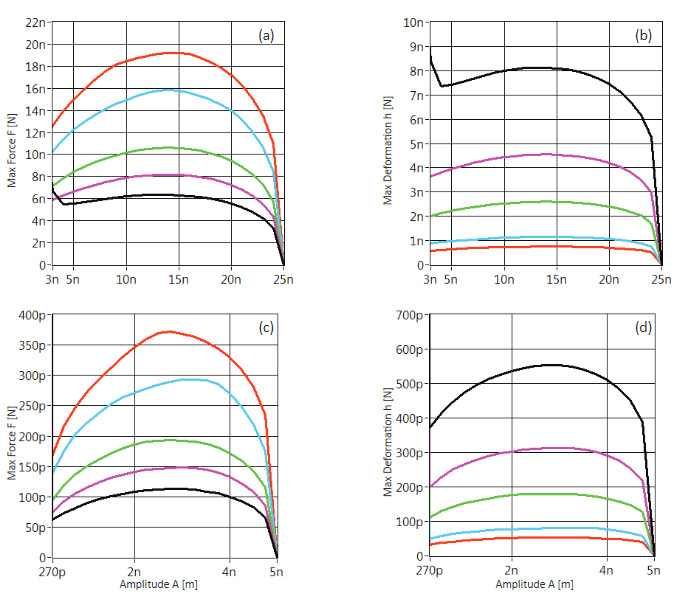
Рис. 7. Результаты численного моделирования зависимостей максимальной силы и максимальной деформации от амплитуды колебаний при различных значениях Asp и A0 для метода АМ. Графики (a)-(b) получены для зонда с k=40 Н/мкм, Q=350, R=10 нм при A0=25 нм. Графики (c)-(d) получены для зонда с k=0.5 Н/мкм, Q=80, R=10 нм при A0=5 нм. Соответствие цветов кривых и значений модуля упругости материала: черный - 65 МПа, розовый - 200 МПа, зеленый - 600 МПа, синий - 3 ГПа, красный - 7 ГПа
Максимальная сила воздействия на зонд для прерывистого контакта вычисляется по формуле Герца при h = maxh.
В рамках этого подхода мы провели численное моделирование максимальной силы воздействия на зонд и деформации образца для трех типов датчиков, используемых при работе с методами АМ-АСМ и П-АСМ [15] (CGS 30 - жесткость ~0.5 Н/мкм, NSG01 - жесткость ~2 Н/мкм, NSG30 - жесткость ~40 Н/мкм), и пяти модельных образцов с различными значениями модуля упругости (65 МПа, 200 МПа, 600 МПа, 3 ГПа и 7 ГПа).
Полученные результаты по зависимости максимальной деформации от приложенной силы для этих образцов и зондов со значениями жесткости, равными 40 Н/мкм и 0.5 Н/мкм, при значениях амплитуды свободных колебаний 25 нм и 5 нм показаны на Рис. 7a-d. Радиус кривизны острия зонда равен 10 нм (типичное значение для серийных АСМ зондов). Анализ представленных графиков приводит к следующим выводам.
Во-первых, максимальные значения силы и деформации наблюдаются для амплитуд колебаний близких к половине значения A0. Этот результат согласуется с известными данными по смесям компонентов PE различной плотности [12].
Во-вторых, значения максимальной силы и максимальной деформации обратно пропорциональны модулю упругости образца. В-третьих, типичный диапазон силы воздействия на образец в методе АМ-АСМ простирается от 100 пН до 20 нН. Поэтому общий диапазон сил в области малых воздействий для АМ-АСМ и П-АСМ довольно велик.
Однако деформация материала в этих методах занимает разное время, что оказывается существенным при исследовании вязкоупругих материалов (например, полимеров). По этой причине для изучения многих структур лучше всего использовать оба метода (П-АСМ и АМ-АСМ), что подтверждается следующим примером.
В нашей работе по использованию П-АСМ для исследования пленок SBS на подложке Si, которые были получены центробежным нанесением раствора блок-сополимера в толуоле при комнатной температуре, было показано, что поверхность этих образцов легко продавливается и даже модифицируется под воздействием зондов со значениями жесткости 4 Н/мкм и 40 Н/мкм [14].
Если же обогатить верхний слой такой пленки блоками полибутадиенового каучука, имеющими низкую поверхностную энергию, то она не повреждается при измерениях по методу АМ-АСМ, а контакт с зондом приводит к обратимой деформации образца [16]. Аналогичный результат был получен для П-АСМ при использовании датчика с жесткостью 0.5 Н/мкм. С помощью этого зонда для одного и того же участка пленки SBS были получены изображения с применением АМ-АСМ и П-АСМ (Рис. 8a-b), которые практически не отличаются.
Наблюдаемая на этих изображениях разупорядоченная морфология заметно отличается от упорядоченной структуры с разделением микрофаз, характерной для приповерхностной организации этой пленки. Если пленка SBS изготовлена по методу горячего центробежного нанесения, разделение микрофаз происходит более эффективно, и на изображении рельефа, полученному с помощью АМ-АСМ с датчиком, имеющим жесткость 0.5 Н/мкм, видна характерная картина упорядочения.

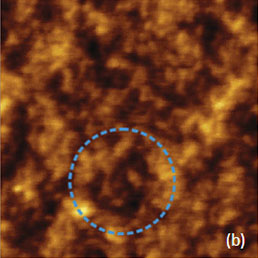



Фазовое изображение для этого участка (на рисунке не показано) не выявило деталей структуры из-за малости приложенной силы.
Изображение рельефа от него же, полученное с помощью П-АСМ при малой силе воздействия, имеет обращенный контраст, что видно из сравнения областей, ограниченных синими окружностями.
Отметим, что контраст микрофаз наблюдается на изображении по адгезионным силам, но отсутствует на изображении по жесткости. Поэтому обращение контраста на изображениях по высоте при переходе от П-АСМ к АМ-АСМ может объясняться влиянием адгезионных сил.
Этот пример указывает на необходимость решения проблемы, которая заключается в том, что постоянство отклонения кантилевера в процессе сканирование поверхности не гарантирует равенства деформации поверхности в точках контакта, если адгезионные силы в этих точках различны. Поэтому П-АСМ требует дальнейшей доработки как в плане визуализации, так и в плане исследования его работы в областях высоких и низких сил воздействия на образец.
РАСШИРЕНИЕ ВОЗМОЖНОСТЕЙ ВИЗУАЛИЗАЦИИ ПОВЕРХНОСТНЫХ СТРУКТУР С ПОМОЩЬЮ П-АСМ









Визуализация поверхностных структур - одна из основных задач АСМ. Для изучения мягких неоднородных материалов можно использовать изображения высокого контраста, обеспечиваемые методом АМ-АСМ с повышенной силой воздействия.
Этот подход показал свою эффективность в исследовании ламеллярного упорядочения полукристаллических полимеров, в которых аморфный компонент находится в эластичном состоянии, зависящем от внешних условий. Увеличение силы воздействия со стороны АС зонда приводит к аморфных продавливанию областей между ламелями, на фоне которых сами ламели становятся хорошо различимы. Отметим, что изображения рельефа ряда образцов полиэтилена (polyethylene, PE), полученные с помощью П-АСМ, имеют намного лучший контраст, чем изображения от тех же образцов, полученные по методу АМ-АСМ с повышенной силой прижима. Этот факт демонстрируется Рис. 9a-c, на которых представлены изображения рельефа образцов линейного полиэтилена низкой плотности (linear low density polyethylene, LLDPE), полученные с помощью АМ-АСМ и П-АСМ. Ламели имеют толщину 10-20 нм, а ориентация их плоскостей преимущественно вертикальная. Заметно, что разрешение П-АСМ изображений выше, чем АМ-АСМ изображений. Это обусловлено, по-видимому, тем, что в П-АСМ зонд сильнее воздействует на аморфные участки.
Эта деформация обратима, поскольку на АМ-АСМ изображении, полученном после получения П-АСМ изображения, повреждений поверхности не наблюдается. Линейная конформация полимерных цепей LLDPE способствует их сворачиванию и формированию протяженных ламелей, что характерно для этого материала, имеющего плотность 0.91-0.93 г/см3 и модуль упругости 400-700 МПа. Формирование ламеллярных сеточных структур с более короткими компонентами наблюдается и в образцах PE, для молекул которого характерно наличие множественных октеновых ветвлений в линейных цепях. Подобные материалы имеют низкую плотность (0.88 0.86 г/см3) и высокую эластичность при модуле упругости ниже 70 МПа. Морфология пленок из этих материалов, изготовленных из PE с плотностями 0.86 г/см3 (PE/0.86) и 0.87 г/см3, была исследована с помощью АМ-АСМ и П-АСМ (Рис. 9d-h).
Как и в случае LLDPE, П-АСМ обеспечивает более высокое разрешение при визуализации ламеллярного упорядочения. Как и ожидалось отдельные ламели образца PE/0.86 оказались короче, а их концентрация ниже. П-АСМ изображения имеют высокий контраст, и поэтому их можно использовать для количественного анализа кристалличности образцов PE путем оценки площади, занятой ламелярными структурами.
Изучение ламеллярного упорядочения в пленках PE не исчерпывает все достоинства П-АСМ, относящиеся к визуализации поверхностных структур. С помощью П-АСМ были получены хорошие результаты по упорядочению цепей в гребнеобразных молекулах на основе poly(n-butyl acrylate), показанные на Рис. 10a-f. Этот объект стал предметом интенсивного исследования с помощью АСМ, поскольку в нем происходит спонтанное разрушение ковалентных связей в ходе адсорбции на подложке; см. по этому вопросу [17] и представленную там литературу. В своей работе мы исследовали несколько гребнеобразных молекул, из которых были получены пленки на слюде методом Ленгмюра-Блоджетт (ЛБ).
Линейные цепи гребнеобразных молекул выглядят на АМ-АСМ изображениях как протяженные полосы шириной 30 нм и высотой 5 нм.


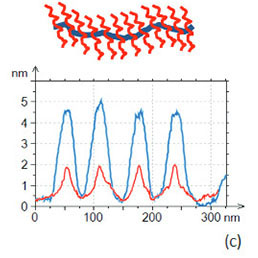


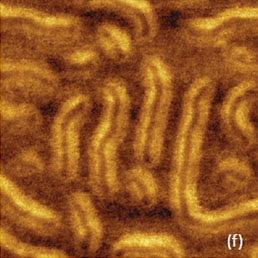
П-АСМ изображения этих объектов оказались боле детализированными. На них видна сердцевина макромолекул шириной ~6 нм и более темные периферийные области по обе стороны от серцевины, которые, по-видимому, соответствуют боковым цепям. Увеличенные изображения аналогичных участков показаны на Рис. 10d‑e.
Профили поперечного сечения макромолекул по П-АСМ изображению соответствуют объектам с провалом 2 нм по высоте. Это указывает на значительную деформацию макромолекул под воздействием АСМ зонда в П-АСМ, которая помогает выявить структуру этих гребнеобразных макромолекул.
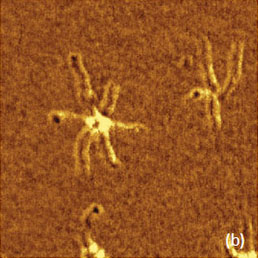
На изображении распределения адгезионных сил (Рис. 10f) видна та же структура макромолекул, состоящая из хорошо отличающихся сердцевины и боковых цепей. Влияние адгезионных сил на поведение системы, включающей кончик зонда и макромолекулы, размеры которых сопоставимы, требует отдельного рассмотрения. После изучения макромолекул с линейной и звездообразной геометрией становится актуальной задача визуализации разветвленных макромолекул с короткими боковыми цепями.
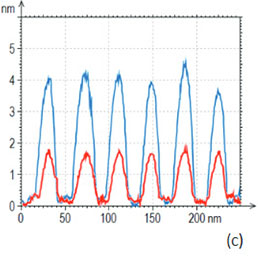
На Рис. 11a-e представлены изображения одного и того же участка ЛБ пленки, состоящей из линейных макромолекул, полученные с помощью АМ АСМ и П АСМ. На изображениях рельефа, полученных с их помощью (Рис. 11a и 11d), видны протяженные структуры, на поперечных сечениях которых заметен провал (Рис. 11c), который более глубок в случае П-АСМ.
Контраст фазового изображения (Рис. 11b) позволяет различить макромолекулы и подложку, а адгезионное изображение оказалось наиболее детализированным. Яркие периферийные области протяженных структур, соответствующих сердцевинам макромолекул, относятся к коротким боковым цепям.В отличие от молекул с длинными боковыми цепями, на изображении рельефа, полученном с помощью П-АСМ, короткие боковые цепи не видны.
В отличие от молекул с длинными боковыми цепями, на изображении по высоте, полученном с помощью П-АСМ, короткие боковые цепи не видны.




Как показывает другой пример гребнеобразных молекул, для различения сердцевины и боковых цепей более информативными оказываются изображения по адгезионным силам и по жесткости. Изображения получены от звездообразных макромолекул, имеющих гребнеобразные лучи. Сравнение контраста изображений по высоте и изобржений по адгезионным силам и жесткости доказывает, что последние имеют более высокую чувствительность к деталям структуры макромолекул.
Экспериментальные данные, представленные в этом разделе статьи, доказывают, что с помощью П-АСМ можно существенно повысить качество визуализации деталей ламеллярного упорядочения и гребнеобразных макромолекул.


КАРТИРОВАНИЕ ЛОКАЛЬНЫХ МЕХАНИЧЕСКИХ СВОЙСТВ БИНАРНЫХ СМЕСЕЙ ПОЛИМЕРОВ
Очевидным преимуществом П-АСМ по сравнению с другими АСМ методами является возможность картирования распределения адгезионных сил и жесткости в режиме реального времени. Эта возможность особенно интересна для применений, связанных с неоднородными материалами, для которых, наряду с картированием по составу, зачастую требуются не только количественные измерения характеристик для компонентов материала, но и для границ раздела, которые могут иметь решающее влияние на свойства материала.
Ниже будет рассмотрено картирование адгезионных сил и жесткости для нескольких бинарных смесей полимеров, список которых приведен в Табл. 1. Там же указаны значения модулей упругости для макроскопических образцов. Диапазон значений модуля упругости полимеров довольно широк - от 16 МПа до 7 ГПа. В своей работе мы исследовали также бинарные сплавы металлов Bi и Sn, имеющими значения модуля упругости 32 ГПа и 50 ГПа, соответственно. Полимеры, перечисленные в Табл. 1, существуют в аморфном и полукристаллическом состояниях.
В случае полукристаллических материалов макроскопические упругие свойства определяются как ламеллярной, так и аморфной, компонентами, и вариация модуля упругости в широком диапазоне значений оказывается возможной вследствие различий в морфологии и в концентрации кристаллического компонента. Как уже было показано на примере образцов PE (Рис. 9a-i), наблюдаемая вариация локальных механических свойств на наноуровне обусловлена различиями взаимодействия зонда с ламелями и с аморфными областями.
Табл. 1. Полимеры, использованные в бинарных смесях и их модули упругости
| Полимер (наименование и аббревиатура) | Модуль упругости |
|---|---|
| Polybutadiene, PBD | 16 MPa |
| Polyethylene with octene branches, PE/0.86 | 16 MPa |
| Polyethylene with octene branches, PE/0.87 | 65 MPa |
| Low-density polyethylene, LDPE | 152-290 MPa |
| Linear low-density polyethylene, LLDPE | 140 MPa -1.5 GPa |
| Poly(methyl methacrylate), PMMA | 2.4 GPa |
| Poly(vinyledene fluoride), PVDF | 2.4 GPa |
| Atactic polystyrene, PS | 3.0-3.5 GPa |
| Syndiotactic polystyrene, sPS | 7.0 GPa |
Эту особенность полукристаллических полимеров необходимо учитывать при сравнении макроскопических и локальных механических характеристик.
Полимерные пленочные образцы, исследованные в этой работе, были изготовлены из горячих растворов компонентов в подходящем растворителе, которые наносились центробежным способом на подложки Si при повышенной температуре. Такая процедуры позволила изготовить смеси плохо смешивающихся компонентов, в которых расстояние между областями микрофаз составляло от нескольких десятков нанометров до десятков микрон.
В анализе картирования наномеханических свойств с помощью П-АСМ будут рассмотрены смеси нерегулярного полистирена (Atactic polystyrene, PS) с полибутадиеном (Polybutadiene, PBD) и низкоплотным полиэтиленом (Low-density polyethylene, LDPE) и смесь PBD с PE/0.86.
Морфология смеси PS-PBD, оба компонента которой являются аморфными, характеризуется сферическими и эллиптическими включениями одного компонента в матрице, состоящей из другого компонента (Рис. 13a-f). Размер включений достигает нескольких нанометров. Изображения по высоте для этого образца, полученные по методам АМ-АСМ и П-АСМ (Рис. 13a-b), выглядят практически одинаково, за исключением нескольких моментов. Поперечные сечения доменов (Рис. 13c) показывают, что в случае П-АСМ высота доменов больше.

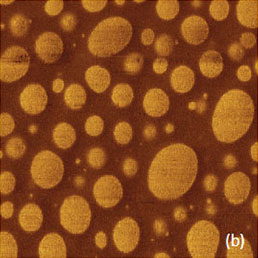
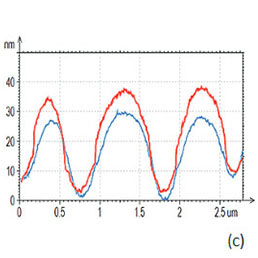


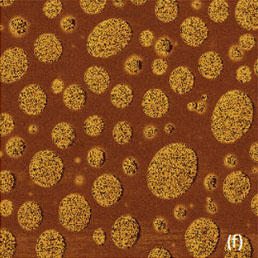
Это означает, что матрица под действием зонда продавливается сильнее, чем домены, и поэтому матрица состоит из более мягкого компонента PBD. Вследствие большего продавливания в П-АСМ на изображениях по высоте хуже видны края доменов. На фазовом изображении, полученном с помощью АМ-АСМ, компоненты смеси хорошо различимы, однако по нему трудно определить соответствие областей и компонентов и оценить значение характеристик материала.
Указанная проблема легко решается с помощью изображений по адгезионным силам и жесткости (Рис. 13e-f), поскольку области высокой жесткости и низкой адгезии относятся к участкам с преобладанием PS. Количественный анализ механических свойств по данным АСМ опирается на кривые DvZ и значения параметров зонда. В принципе, имеющиеся в настоящее время возможности по сбору данных и анализу этих кривых в режиме реального времени позволяют оперативно отображать результаты количественного анализа.
Однако остаются проблемы интерпретации этих кривых, полученных с помощью П-АСМ, как показывает пример смеси PS-PBD, показанный на Рис. 14a-b. Кривые DvZ как для участка S, так и для участка PBD, полученные при сравнительно низком уровне рабочей точки, заметно отличаются в случаях подвода и отвода зонда.
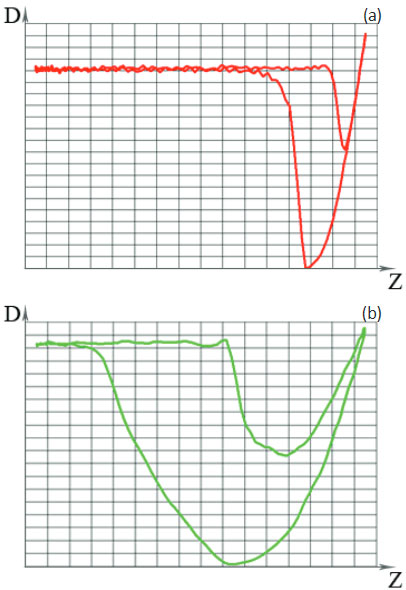
Рис. 14. Кривые DvZ, полученные на участках PS и PBD, соответственно
Наклоны кривых подвода и отвода для PS одинаковы, что означает обратимость деформации образца под действием зонда. Подобное поведение, характерное для эластичных полимеров, может быть описано в рамках моделей упругой деформации твердых тел (DMT, JKR, Sneddon), а значения модуля упругости и работы адгезии для подходящей модели хорошо согласуется с данными для макроскопических образцов, как было показано нами в одной из предыдущих работ [18].
Участок PBD при деформации ведет себя совершенно по-другому - судя по различию наклонов кривых подвода и отвода, этот процесс сопровождается диссипацией энергии. Этот результат можно объяснить тем, что полимеры PS и PBD имеют не только различные значения модуля упругости, но и значения модуля вязкоупругости.
Мерой вязкоупругости полимерных материалов служит параметр tanδ, который равен отношению диссипативной и консервативной компонент комплексно-значного модуля упругости. Значения этого параметра для PBD (tanδ = 0.6) и для PS (tanδ = 0.02) существенно отличаются. К сожалению, к настоящему времени адекватной модели вязкоупругих свойств, применимой к анализу данных АСМ, не создано. Поэтому количественная интерпретация данных изображений по адгезионные силам и жесткости в терминах механических свойств остается нерешенной проблемой.
Дальнейший анализ картирования по адгезионным силам и жесткости будет проводиться на примерах смесей PS-LDPE и PBD-PE/0.86. Эти смеси состоят из несмешивающихся полимеров, один из которых находится в полукристаллическом, а второй - в аморфном, состояниях. Анализ изображений образцов такого состава облегчается тем, что на них хорошо видны ламеллярные структуры, которые соответствуют одному из компонентов смеси.


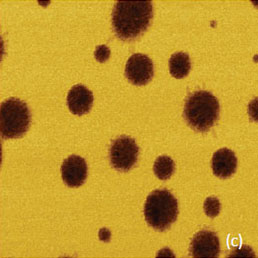
На П-АСМ изображениях смеси PS-LDPE наблюдаются сферические включения в аморфной матрице (Рис. 15a-c). Ламелярная структура включений указывает на то, что в них преобладает LDPE, а их низкая жесткость соответствует сравнительной мягкости этого компонента. Подтверждается также предположение о том, что при повышении силы прижима зонда включения продавливаются сильнее, чем окружающая матрица, состоящая в основном из PS.
Особенностью визуализации образца смеси PBD-PE/0.86 с использованием П-АСМ является тот факт, что компоненты этой смеси имеют близкие значения макроскопического модуля упругости, равные ~16 МПа, при существенно различающихся значениях параметра вязкоупругости: для PE/0.86 tanδ = 0.25, что значительно меньше, чем значение этого параметра для PBD. Изображения образцов этой смеси, полученные по методам АМ-АСМ и П-АСМ, представлены на Рис. 16a-e. Как и в предыдущем примере, изображения по высоте аналогичны для обоих методов, а на изображениях по фазе, адгезионным силам и жесткости хорошо видны области различных микрофаз.




Данные изображения распределения жесткости с большим увеличением (здесь не приведено) указывают на наличие ламеллярных структур внутри темных сферических доменов и, тем самым, на их соответствие участкам полукристаллического PE/0.86. Этот пример подчеркивает необходимость хорошего понимания того, как локальная вязкоупругость влияет на изображения распределений адгезионных сил, жесткости и фазы.
В сочетании с адаптивной системой онлайн анализа силовых кривых, которая предоставит возможность подбора адекватной механической модели материала, это позволит создать прибор, в котором реализован полностью автоматизированный количественный анализ наномеханических свойств.
СОВМЕСТНОЕ ПРОВЕДЕНИЕ ИЗМЕРЕНИЙ ЛОКАЛЬНЫХ МЕХАНИЧЕСКИХ И ЭЛЕКТРИЧЕСКИХ СВОЙСТВ
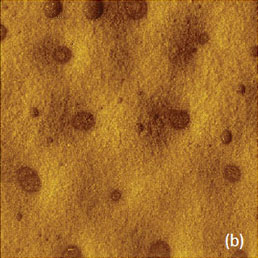
Спектр объектов для изучения локальных механических свойств не ограничивается полимерами, для которых модуль упругости обычно не превышает значения 10 ГПа. При использовании жестких зондов, имеющих значение упругой постоянной на уровне 200 Н/мкм и выше, с помощью П-АСМ можно проводить исследование металлических образцов, например, сплава неполного состава Bi и Sn. Изображения рельефа и жесткости такого образца, полученного путем горячего плавления между двумя слюдяными поверхностями, представлены на Рис. 17a-b.



Рельеф образца сравнительно плоский, на нём наблюдаются контуры, соответствующие границам кристаллических доменов. На карте жесткости также видны границы доменов. Более яркие домены, по-видимому, соответствуют Sn, который имеет более высокое значение модуля упругости (50 ГПа) по сравнению с Bi (32 ГПа). Этот вывод подтверждается данными Кельвин-зондовой силовой микроскопии (КЗСМ), которая позволяет измерить локальную работу выхода материалов. Измерения с помощью однопроходной КЗСМ проводились с использованием проводящего зонда, имеющего жесткость 2 Н/мкм (Рис. 17c-d). Контраст поверхностного потенциала, как и контраст карты жесткости, имеет два уровня значений. Это подтверждает наше предположение о том, что домены относятся к двум различным металлам. Кроме того, разность поверхностных потенциалов доменов близка к разности работ выхода компонентов сплава Bi (4.22 В) и Sn (4.42 В).
Рассмотренное изображение распределения поверхностного потенциала сплава Bi и Sn было дополнено данными однопроходной КЗСМ с фазовой модуляцией (ФМ), которая используется для регистрации силы электростатического взаимодействия между зондом и образцом. Этот метод обеспечивает более высокие разрешение и точность по сравнению с другими методами КЗСМ, что подтверждается результатами, представленными на Рис. 18a-d.



Одной из проблем реализации этих методов является продолжение регистрации электростатической силы взаимодействия между зондом и образцом после отвода, даже когда зонд находится далеко от поверхности образца.
То же относится и к регистрации базового уровня в П-АСМ, что снижает его привлекательность по сравнению с однопроходным методом, в котором зонд находится близи от поверхности все время в процессе измерений.
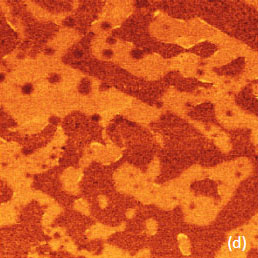
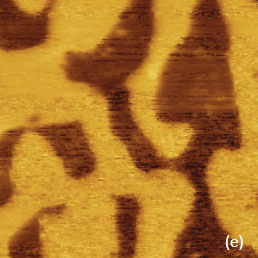
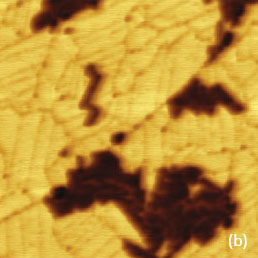
Сочетание информации о структуре и информации о локальных механических и электрических свойствах обеспечивает полноту АСМ исследований материалов, что видно по результатам, представленным на Рис. 19-20. Здесь показаны изображения одного и того же участка образца самосборки полуфторированных алканов [CF3(CF2)14(CH3)20CH3] на графите. На Рис. 19a-d показаны П-АСМ изображения по адгезионным силам и жесткости, а на Рис. 20a-d - АМ-АСМ изображения по поверхностному потенциалу и по градиенту емкости.
Рельеф образца определяется плоскими ламелями фторалканов, лежащих на подложке, и островками самосборок, состоящих из протяженных блоков толщиной 4 нм и спиралей. В ламелях молекулы уложены в плоскостях ламелей, а в самосборках имеют преимущественно вертикальную ориентацию, причем фторированные сегменты находятся вдали от подложки [19]. Особенности топографической и молекулярной организации определяют механические и электрические свойства образца. Ламели лежат непосредственно на подложке, их эффективная жесткость больше, чем жесткость самосборок, расположенных выше (Рис. 19c).
В большинстве самосборок фторированные группы сконцентрированы на верхней поверхности, в то время как на поверхности ламелей количество фторированных и гидрогенизированных участков приблизительно одинаково. Эти химические различия проявляются на распределении адгезионных сил, на котором области самосборок имеют более низкую адгезионную способность (Рис. 19b).
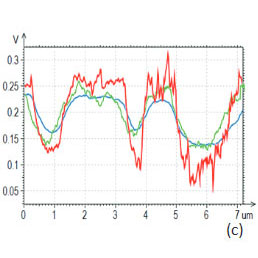
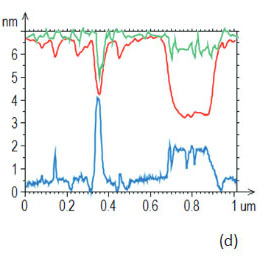
На Рис. 19d показаны одномерные профили сечений изображений по высоте, адгезионным силам и жесткости. Полученные от того же участка образца изображения по поверхностному потенциалу и dC/dZ представлены на Рис. 20b-c.
Главным фактором, определяющим контраст по поверхностному потенциалу, является ориентация молекулярных диполей. В областях самосборок поверхностный потенциал имеет отрицательные значения (~-0.8 В) вследствие вертикальной ориентации диполей в центральных узлах -CH2-CF2 и концевых группах - CF3 [18]. Контраст изображения по dC/dZ имеет более сложную природу, поскольку он определяется не только диэлектрическими свойствами материала, но и толщиной объекта.



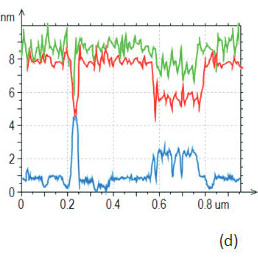
Поэтому контрасты одного и того же локального объекта на изображениях рельефа, распределений поверхностного потенциала и dC/dZ могут существенно различаться, что можно видеть на примере высокого протяженного блока, выделенного на изображении окружностью красного цвета. Этот блок выглядит более темным по сравнению с другими самосборками на изображении dC/dZ, поскольку его высота больше.
На Рис. 20d проводится сравнение локальных различий изображений рельефа, поверхностного потенциала и dC/dZ с помощью одномерных сечений.
Выше обсуждалась возможность проведения количественного анализа наномеханических данных на основе распределения адгезионных сил и жесткости. Здесь следует сказать, что количественный анализ электрических данных также имеет большое значение.
В случае поверхностного потенциала, который можно измерить непосредственно, основной проблемой остается воспроизводимость измерений во внешней среде, для которых в случае однопроходных методов более надежным результатом является значение разности потенциалов, а не их абсолютная величины.
Для получения количественных значений диэлектрической проницаемости необходимо провести численную обработку данных с использованием значения толщины объекта. В этом направлении уже проведены первые работы, и для сверхтонких пленок PS и poly(vinyl acetate) на проводящем стекле получены распределения диэлектрической проницаемости [20].


ЗАКЛЮЧЕНИЕ
В этой статье приведена общая информация о П-АСМ и на ряде примеров показаны её возможности и преимущества по сравнению с АМ-АСМ. На основании проведённого анализа можно сделать следующие выводы. П-АСМ применима для исследования широкого спектра образцов при воздействии на них со стороны зонда примерно на том же уровне, что и в АМ-АСМ.
Однако ряд специфических и не всегда верно понимаемых особенностей взаимодействия между зондом и образцом при использовании П-АСМ делают её ценным расширением спектра АСМ методик. Как мы показали на нескольких примерах, контраст изображений, получаемых с её помощью, очень высок и позволяет получать АСМ изображения наноструктур и молекулярных объектов. Кроме того, П-АСМ создает новые возможности в области исследования локальных механических свойств: она обеспечивает высокое разрешение картирования адгезионных сил и жесткости, а в перспективе может стать основой для создания систем адаптивного количественного анализа наномеханических данных для изучения упругих и вязкоупругих свойств полимерных материалов. Наконец, сочетание потенциала П-АСМ для изучения наномеханических свойств и возможностей одночастотных и многочастотных методов АМ-АСМ для изучения электрических свойств на основе количественного анализа электрических данных представляется наиболее интересным в качестве основы системы всеобъемлющего АСМ анализа.
БЛАГОДАРНОСТИ
Автор благодарит проф. M. Moeller (DWI, Aachen, Germany) и проф. S. Sheiko (UNC, Chapel Hill, NC), а также проф. Kuljanishvili (SLU, Saint Louis, MO) и проф. V. Papkov (ИНЭОС, Москва) а предоставление образцов полуфторированных алканов, гребнеобразных макромолекул, углеродных нанотрубок и полимера PDES. Д-р С. Леесмент оказал помощь в получении данных по сплаву Bi/Sn. Хочется также выразить признательность своим коллегам по NT-MDT Development Inc., включая Dr. S. Belikov, Dr. C. Wall и J. Alexander, за постоянную поддержку и помощь в подготовке данных и написании этой статьи.
REFERENCES
1. Y. Martin, C. C. Williams, and H. K. Wickramasinghe “Atomic force microscope-force mapping and profiling on a sub 100-Å scale” J. Appl. Phys. 1987, 61, 4723–4729.
2. Q. Zhong, D. Innis, K. Kjoller, and V. Elings “Fractured polymer/silica fiber surface studied by tapping mode atomic force microscopy” Surf. Sci. Lett. 1993, 290, L688–L692.
3. H. Becker, O. Bender, B. H. vor der Hone, L. Bergmann, K. Rost and A. Zobel “Stylus profiler featuring an oscillating probe” US Patent
2728222, issued Dec. 27, 1955.
4. V. B. Elings, and J. A. Gurley “Jumping probe microscope” US Patent 5,229,606, 1993 (filled 1989).
5. S. Magonov “NEXT Visualization of Surface Structures” Application Note 086, NT-MDT Spectrum Instruments. It can be downloaded from https://www.ntmdt-si.com/resources/applications
6. S. Magonov “AFM-based Electrostatic Modes” Application Note 084, NT-MDT Spectrum Instruments.
It can be downloaded from https://www.ntmdt-si.com/resources/applications
7. S. Magonov “Piezoresponse Force Microscopy in Its Applications” Application Note 083, NT-MDT Spectrum Instruments. It can be downloaded from https://www.ntmdt-si.com/resources/applications
8. A. L. Weisenhorn, P. K. Hansma, T. R. Albrecht, and C. F. Quate “Forces in atomic force microscopy in air and water” Appl. Phys. Lett. 1989, 54, 2651-2653.
9. N. A. Burnham, and R. J. Colton “Measuring the nanomechanical properties and surface forces of materials using an atomic force microscope” J. Vac. Sci. Technol. A 1989, 7, 29 06–2913.
10. S. N. Magonov, V. Elings, and V. S. Papkov “AFM Study of Thermotropic Structural Transitions of Poly(diethylsiloxane)” Polymer 1997, 38, 297-307.
11. Yu. K. Godovsky, V. S. Papkov, and S. N. Magonov “Atomic force microscopy visualization of morphology changes resulting from the phase transitions in polydi-n-alkylsiloxanes: Polydiethylsiloxane” Macromolecules 2001, 34, 976-990.
12. S. N. Magonov “AFM in Analysis of Polymers” Encyclopedia of Analytical Chemistry, (R. A. Meyers, Ed.), pp. 7432-7491, John Willey & Sons Ltd, Chichester, 2000.
13. S. Belikov and S. Magonov “Classification of Dynamic Atomic Force Microscopy Control Modes Based on Asymptotic Nonlinear Mechanics” Proceedings American Control Society, St. Louis, 979-985, 2009.
14. S. Belikov, J. Alexander, C. Wall, and S. Magonov “Tip-Sample Forces in Atomic Force Microscopy: Interplay between Theory and Experiment” Fall 2012 MRS Meeting Proceedings, 2013, in press.
15. www.ntmdt-tips.com
16. S. N. Magonov, V. Elings, J. Cleveland, D. Denley, and M. H. Whangbo “Tapping-mode atomic force microscopy study of the near-surface composition of a styrene-butadiene-styrene triblock copolymer film” Surface Science 1997, 389, 201-211.
17. N. V. Lebedeva, A. Nese, F. C. Sun, K. Matyjaszewski, and S. S. Sheiko “Anti-Arrhenius cleavage of covalent bonds in bottlebrush macromolecules on substrate” PNAS 2012, 109, 9276-9280.
18. S. Magonov “Exploring Nanomechanical Properties of Materials with Atomic Force Microscopy” Application Note 085, NT-MDT Spectrum Instruments. It can be downloaded from https://www.ntmdt-si.com/resources/applications
19. J. Alexander, S. Magonov, and M. Moeller “Topography and surface potential in Kelvin force microscopy of perfluoroalkyl alkane self-assemblies” JVST B 2009 B27 (2), 903-911.
20. S. Belikov, J. Alexander, S. Magonov, and I. Yermolenko “Towards quantitative local dielectric analysis of polymers” Amer. Control Conference 2012, 3228-3233.
* Метод П-АСМ с низкочастотными колебаниями образца реализован в приборах НЕКСТ II, ИНТЕГРА, ИНТЕГРА Нано ИК, ИНТЕГРА Спектра II, СОЛВЕР Опен, НАНОЭДЬЮКАТОР II, СОЛВЕР Нано. В приборах ВЕГА, СОЛВЕР Пайп II, СМЕНА применяются низкочастотные колебания АСМ зондом, закрепленным на пьезосканере.