Однопроходные методы в атомно-силовой микроскопии: Кельвин-зондовая силовая микроскопия и измерение локальных диэлектрических свойств
Пример применений 082 (pdf 2.8 Mb)
Сергей Магонов, NT-MDT Development
АННОТАЦИЯ
Рассматривается перспективная методика измерения поверхностного потенциала и диэлектрического отклика, реализованная с помощью однопроходной методики измерений на атомно-силовом микроскопе компании НТ-МДТ Спектрум Инструментс, оснащенном контроллером PX, позволяющим проводить многочастотные АСМ исследования. Проведены измерения локальных электрических свойств с высокой чувствительностью и нанометровым пространственным разрешением при использовании фазово-модуляционной регистрации градиента электростатической силы. Эффективность такого подхода показана на образцах разного типа: самосборках фторалканов, полимерах, металлах и полупроводниках. Полученные результаты показывают применимость использования поверхностного потенциала и диэлектрического отклика для картирования состава гетерогенных материалов. Обсуждаются вопросы, связанные с количественными измерениями поверхностного потенциала. Предложен новый подход к расчету диэлектрической проницаемости по данным АСМ.
ВВЕДЕНИЕ
Последние 25 лет наблюдается бурное развитие атомно-силовой микроскопии (АСМ), в которой появились комбинированные методики, позволяющие с высоким разрешением отображать структуру поверхности образцов, а также исследовать их локальные материальные свойства. Суть АСМ заключается в регистрации, отслеживании и использовании сил взаимодействия зонд-образец для задач определения профиля поверхности образца, измерения его механических или электромагнитных откликов. Зондовый датчик АСМ представляет собой микромеханическую структуру, основу которой составляет закрепленная на чипе гибкая консоль (кантилевер), на свободном конце которой расположен острый пирамидальный зонд. Кантилевер служит чувствительным элементом, измеряющим и индицирующим силу, действующую между кончиком зонда и образцом. В зависимости от метода измерений эта сила приводит к квазистатическому изгибу кантилевера или изменяет динамику его колебаний (частоту, фазу, амплитуду), которые возбуждаются пьезодрайвером, размещенным вблизи зондового датчика. Для регистрации электростатических силовых взаимодействий с образцом зонд АСМ обычно покрывают слоем металла. Достоверное измерение электрических свойств образца требует раздельной регистрации вкладов механического и электростатического взаимодействий. Ниже будет показано, как эту проблему можно решить с помощью однопроходной многочастотной АСМ, которая позволяет одновременно регистрировать рельеф поверхности, поверхностный потенциал и локальный диэлектрический отклик образца. Помимо этого будет показано, как реализуется количественное измерение диэлектрической проницаемости. Используемые подходы основаны на общей теории движения зонда под действием сил, возникающих между зондом и образцом [1]. Стационарный режим колебаний зонда описывается следующими уравнениями:
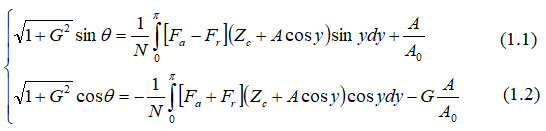
где A и θ – амплитуда и фаза колебаний зонда; A0 – амплитуда колебаний зонда в отсутствие взаимодействия с образцом, Fa, Fr – силы взаимодействия зонд-образец во время выполнения процедур подвода и отвода, Zc – вертикальная координата профиля образца, G – параметр, связанный с текущей и резонансной частотами колебаний зондового датчика ω и ω1 и добротностью Q1:
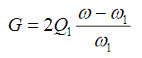
При использовании амплитудно-модуляционного (АМ) метода с ω=ω1 если выполнено условие консервативности взаимодействия (Fa=Fr), эти уравнения приводятся к более простому виду:
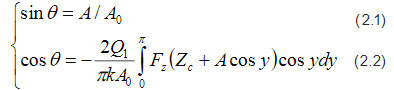
где Fz=Fa= Fr
Если модель силового взаимодействия достаточно реалистична, эти соотношения хорошо описывают поведение зондового датчика для разных методов и режимов АСМ и пригодны для получения механических и электрических характеристик по данным АСМ.
ИЗМЕРЕНИЕ ЭЛЕКТРОСТАТИЧЕСКИХ СИЛ С ПОМОЩЬЮ АСМ
Чувствительность проводящего зондa к электростатической силе использовалась в одной из первых работ по АСМ [2]. В этой революционной работе для бесконтактного измерения рельефа образца использовалась первая изгибная мода резонансных колебаний кантилевера (с частотой ωmech). Одновременно с этим инициировалось электростатическое взаимодействие зонд-образец приложением к зонду переменного напряжения с частотой (ωelec) ниже резонансной. Амплитуда колебаний зонда на частоте (ωelec) отражает вариации электростатической силы, обусловленной поверхностными зарядами и диполями, а также локальной работой выхода, типом и концентрацией легирующей примеси.
Таким образом, отслеживание отклика зондового датчика на двух и более частотах позволяет одновременно и независимо проводить измерения локальных электрических и механических взаимодействий, при этом последние используются для определения рельефа поверхности.
Этот принцип положен в основу однопроходного метода, реализующего параллельную регистрацию поверхностного потенциала с применением Кельвин-зондовой силовой микроскопии (КЗСМ) и производной емкости зонд-образец dC/dZ (Z – расстояние между зондовым датчиком и образцом по вертикали). Теоретической основой для измерения поверхностного потенциала и dC/dZ служит уравнение емкостной модели электростатического взаимодействия зонда и образца [2]. Квадратичная зависимость силы этого взаимодействия от разности поверхностных потенциалов зонда и образца приводит к появлению нескольких силовых компонент, когда к зонду прикладывается смещение с постоянной UDC и переменной UAC (с частотой ωelec) составляющими
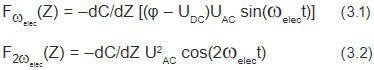
В уравнении (3.1) 𝜑 является разностью поверхностных потенциалов зонда и образца под зондом (контактной разностью потенциалов). Эту разность можно определить, подстроив постоянную компоненту напряжения смещения UDC таким образом, чтобы амплитуда компоненты с частотой ωelec обратилась в ноль. Эта задача решается с помощью схемы слежения КЗСМ. Производная емкости dC/dZ прямо пропорциональна амплитуде второй гармоники электростатической силы (с частотой 2ωelec), она связана с диэлектрической проницаемостью (ε) материала на участке, расположенном под зондом. Для многих материалов диэлектрическая проницаемость является комплексной величиной, поэтому необходимо измерять как действительную, так и мнимую части dC/dZ. В нашем рассмотрении не учитывается зависимость емкости от приложенного напряжения, но, как было показано в [3], производная dC/dV может быть найдена по амплитуде компоненты с частотой 3ωelec. Как видно из приведенного рассмотрения, схема измерений с набором синхронных детекторов, настроенных на частоты ωmech, ωelec, 2ωelec и 3ωelec, позволяет одновременно измерять рельеф поверхности и различные электрические и диэлектрические характеристики образца.
Подобный подход с использованием нескольких частот во многих отношениях предпочтительнее популярных двухпроходных методов, в которых сначала производится измерение рельефа, а затем зонд отводится от образца на расстояние 10–20 нм и измеряется распределение электрических свойств [4]. Двухпроходные методы сравнительно просты в реализации, но имеют ряд недостатков: (a) искажающее влияние электростатического взаимодействия зонд-образец на формирование изображения рельефа; (b) трудность подбора расстояния, на которое отводится зонд перед вторым проходом для исключения механического взаимодействия с неровной поверхностью; (c) ухудшение пространственного разрешения и чувствительности вследствие удаленности зонда от образца. Последнее ограничение устраняется применением однопроходной методики за счет расположения зонда близко к образцу. К настоящему времени преимущества однопроходной схемы измерений доказаны экспериментально [5-6].
РЕАЛИЗАЦИЯ КЗСМ И ИССЛЕДОВАНИЯ ДИЭЛЕКТРИЧЕСКИХ СВОЙСТВ В ОДНОПРОХОДНОМ РЕЖИМЕ
Последние достижения в разработке электроники для АСМ позволяют реализовать многочастотные измерения и возбуждение различных колебательных мод кантилевера, расширяя тем самым возможности организации оптимальных методик для углубленного изучения поверхностных характеристик образца. Комбинации амплитудной модуляции (АМ) и частотной модуляции (ЧМ) были использованы для измерения рельефа и КЗСМ картирования в условиях сверхвысокого вакуума [7, 8]. Наибольшая чувствительность и точность измерения поверхностного потенциала были достигнуты с применением ЧМ детектирования градиента электростатической силы. Этот результат согласуется с теоретическими расчетами [9], согласно которым электростатическая сила, действующая на зондовый датчик, определяется не только кончиком зонда, но и кантилевером и зондом в целом. Однако вклады последних факторов можно исключить, если измерять градиент силы. Далее будут представлены экспериментальные результаты, подтверждающие это предположение для стандартных зондов длиной ~10 мкм. Вместе с тем, при использовании очень длинных проводящих зондов (~100 мкм) различие в данных по поверхностному потенциалу, полученных путем измерения силы и путем измерения градиента силы, оказалось мало заметным.
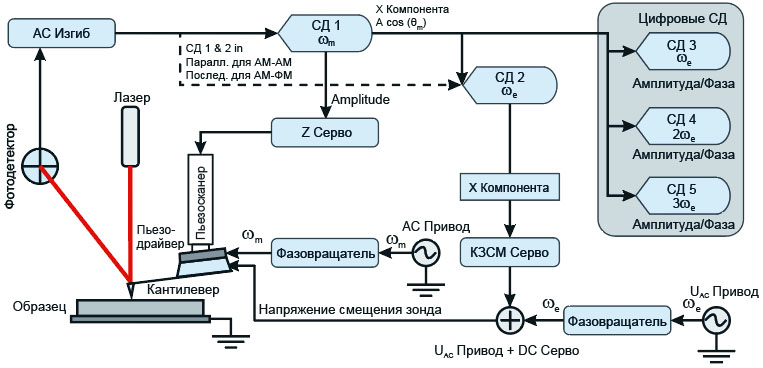
КЗСМ исследования в обычных условиях мы проводили с использованием силы и градиента силы для измерений поверхностного потенциала и диэлектрического отклика. Если зондовый датчик приводится пьезодрайвером в колебательное состояние с частотой ωelec (ωelec⪡ωmech), можно одновременно наблюдать различные частотные компоненты сигнала фотодетектора, если задействовать параллельно соответствующее количество синхронных детекторов (СД). В этом случае для регистрации рельефа поверхности образца поддерживается заданная амплитуда колебаний (Asp), измеряемая настроенным на частоту ωmech первым СД. Настроенный на частоту ωelec второй СД регистрирует амплитуду колебаний, пропорциональную Fωelec(Z). С помощью схемы слежения, входящей в измерительный контур, включающий зондовый датчик, фотодетектор и второй СД, регулируя UDC можно [уравнение (1)] привести к нулю амплитуду колебаний на частоте ωelec и по соответствующей величине UDC определить потенциал - 𝜑. Эту модификацию КЗСМ часто называют КЗСМ-АМ для указания на то обстоятельство, что измеряется электростатическая сила Fωelec. При параллельном использовании двух СД настройка второго СД на частоту 2ωelec дает возможность регистрировать сигнал производной dC/dZ. Амплитуда и фаза (или действительная и мнимая компоненты) этого сигнала существенны для образцов с комплексной диэлектрической проницаемостью. Если добавить в параллель третий СД, то с помощью второго и третьего детекторов можно измерять гармоники на частотах ωelec и 2ωelec, что позволяет одновременно регистрировать рельеф поверхности образца, а также распределения поверхностного потенциала и производной емкости dC/dZ.
В другой схеме измерения поверхностного потенциала и dC/dZ второй и третий СД включаются последовательно с первым (см. Рис. 1), а не параллельно ему, как в схеме рассмотренной выше. При этом электростатическое взаимодействие индуцируется переменным напряжением с небольшой частотой, которая укладывается в ширину полосы механических колебаний зондового датчика с частотой ωmech. Фаза сигнала фотодетектора является суммой вкладов, обусловленных механическим и электростатическим взаимодействиями между зондом и образцом:
Для большей эффективности учета электростатической силы следует минимизировать вклад механического взаимодействия путем задания значения Asp близким к A0 (амплитуде колебаний зондового датчика при большом удалении от образца). В этом случае
а это означает, что частотные компоненты сигнала фазы могут быть использованы для измерения потенциала поверхности и градиента емкости.
Следует отметить, что фазовая модуляция электростатической силы, используемая в предложенной схеме, приводит к тем же результатам, что и ЧМ, поскольку обе методики при упрощающих предположениях приводят к данным по градиенту силы. Анализ схемы с ЧМ дает для сдвига фазы выражение
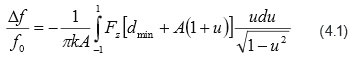
В приближении малых амплитуд его можно упростить с помощью следующего соотношения между частотным сдвигом и градиентом силы [10]:
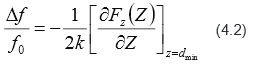
Выражение (2.2), связывающее косинус фазы сигнала и силу взаимодействия зонд-образец, можно использовать и в случае электростатических сил. В приближении малых амплитуд можно получить также простую связь косинуса фазы и градиента силы:
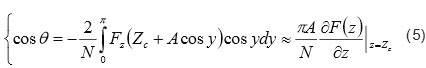
Использование косинуса фазы для обратной связи в КЗСМ более точно рассматривать как КЗСМ-ФМ, где ФМ означает модуляцию фазы градиентом электростатической силы. Таким образом, мы используем КЗСМ-АМ и КЗСМ-ФМ методы, основанные на регистрации электростатической силы и ее градиента, для измерения поверхностного потенциала. Аналогичную схему можно применить для измерений производной dC/dZ, в сочетании с КЗСМ или независимо. Для практической реализации этого подхода имеет большое значение тот факт, что измерения проводятся на разных частотах с использованием амплитудно-модуляционного метода (intermittent contact mode) при минимальном уровне механического взаимодействия зонд-образец. Такие измерения, проведенные на различных образцах, показали, что перекрестные взаимовлияния измерений рельефа и электрических измерений практически отсутствуют [11] .
Ниже рассматриваются различные методики КЗСМ и dC/dZ измерений применительно к разным материалам. Измерения проводились в обычных условиях на сканирующем зондовом микроскопе ИНТЕГРА Прима с универсальной измерительной головкой и контроллером PX. Для многочастотных измерений было существенно, что частотный отклик зондового датчика мог быть измерен вплоть до частоты 5 МГц. Измерения проводились с помощью серийных проводящих зондовых датчиков от разных производителей (Olympus, MikroMasch и НТ-МДТ СИ).
ПРИМЕНЕНИЕ КЕЛЬВИН-ЗОНДОВОЙ СИЛОВОЙ МИКРОСКОПИИ
Использование различных схем регистрации сигнала в сочетании с развитыми многочастотными методиками позволяет проводить исследования характеристик образца (например, поверхностного потенциала или dC/dZ) разными методами и сравнивать полученные результаты. Проверку исследуемой методики и исследование ее эффективности обычно проводят на стандартных образцах. Для своих экспериментов по КЗСМ мы выбрали самосборки частично фторированных алканов на различных подложках (кремниевая пластина, слюда и графит), полупроводниковые SRAM структуры и биметаллический сплав Bi/Sn.
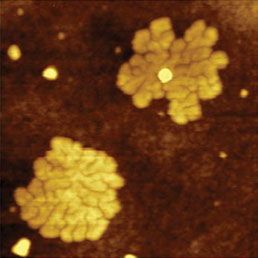
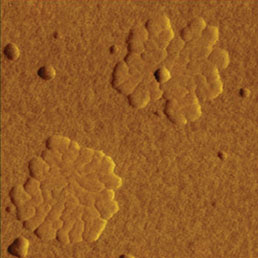


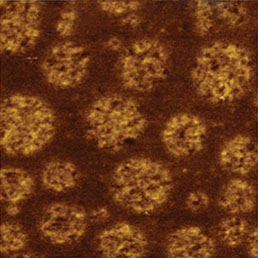
АСМ изображения, иллюстрирующие КЗСМ-ФМ и dC/dZ измерения самосборки частично фторированных алканов CF3(CF2)14(CH2)20CH3 – F14H20 на кремниевой подложке представлены на Рис. 2. На изображениях рельефа и фазы показаны области F14H20 самосборок со спиральной структурой и высотой менее 4 нм. Тот факт, что фазовый контраст выявил только края областей, жесткость которых значительно ниже жесткости подложки, показывает, что измерения по этому методу проводились при малой силе взаимодействия зонда и образца. Как подчеркивалось выше, это одно из главных требований к измерениям по методу КЗСМ-ФМ. Форма самосборки F14H20 на подложке кремниевой отражает разнородность ее молекулярной структуры, а также различие конформаций и объема ее фторированных и гидрогенизированных участков, объединенных ковалентными связями в цепную молекулу. По-видимому, на границе спиралей с воздухом агрегируются более массивные фторированные сегменты [12]. Такая укладка молекул приводит к преимущественно вертикальной ориентации фторалкильных фрагментов с сильным диполем на концевой группе -CF3 и на центральной связи -CF2-CH2-, ориентированной вдоль углеродной цепи.
Это должно приводить к большому отрицательному потенциалу областей F14H20, что было подтверждено изучением ЛБ пленок частично фторированных алканов макроскопическим методом зонда Кельвина [13] и КЗСМ измерений [5-6]. Области заметного отрицательного поверхностного потенциала отчетливо видны на соответствующем изображении распределения поверхностного потенциала Φ, представленном на Рис. 2. Контраст отрицательного потенциала отмечается только на участках с самосборками, в то время как небольшие частицы не визуализируются на изображении поверхностного потенциала. Отсутствие малых частиц на изображении потенциала доказывает, что в используемой однопроходной методике удалось избежать перекрестного влияния каналов измерения механических и электростатических сил. Однако на изображении диэлектрического отклика хорошо видны как участки F14H20, так и эти частицы, наличие которых влияет на производную емкости. Подробнее изображения диэлектрического отклика будут рассмотрены ниже.
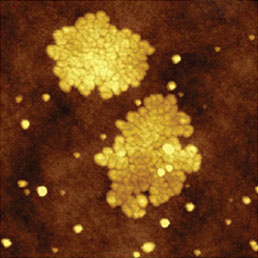
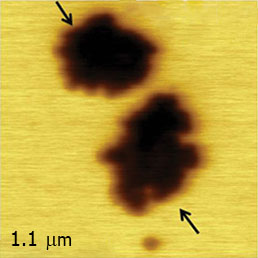
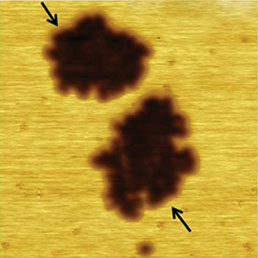

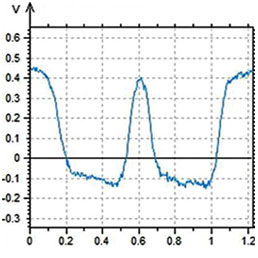
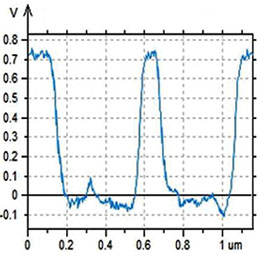
Нами было проведено также сравнение результатов КЗСМ-АМ и КЗСМ-ФМ измерений на одном и том же образце с участками F14H20 на кремниевой подложке (см. Рис. 3). Главное различие полученных результатов заключается в том, что КЗСМ-ФМ дает более сильное падение поверхностного потенциала (–0.8 В) по сравнению с КЗСМ-АМ (–0.6 В). Сравнение профилей потенциалов показывает также, что КЗСМ-ФМ обеспечивает меньшее размытие регистрируемых границ областей самосборок. Величина размытия часто используется в качестве количественной характеристики разрешения в поперечном направлении, и, как видно из представленных данных, этот показатель для КЗСМ-ФМ лучше. Для получения этих изображений использовался зондовый датчик с платиновым покрытием и длиной зонда 10 мкм. Как указывалось во Введении, дальнодействующая сила электростатического взаимодействия между кантилевером и образцом влияет на регистрируемое значение электростатической силы при использовании КЗСМ-АМ, снижая измеряемый уровень поверхностного потенциала и ухудшая пространственное разрешение. Этот эффект мы изучали с помощью специального проводящего зондового датчика, который включал проводящий кантилевер с прикрепленным к нему зондом из графитового волокна, кончик которого был подвергнут химическому травлению. Длина графитового зонда в этом датчике составляла около 100 мкм, и поэтому электростатическое воздействие на образец со стороны кантилевера в этом случае должно быть существенно ниже, чем при использовании стандартного зонда. Это соображение подтверждается данными по КЗСМ-АМ и КЗСМ-ФМ, полученными с помощью этого зонда: в обоих случаях скачок поверхностного потенциала составляет ~–0.8 V (Рис. 4).

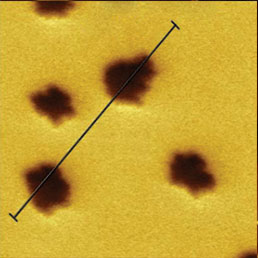
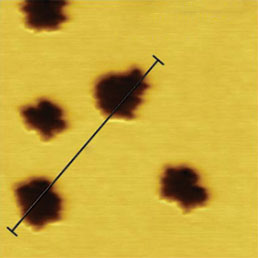

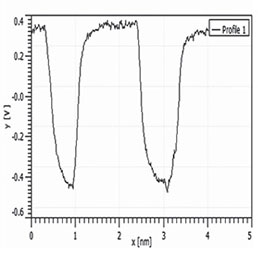
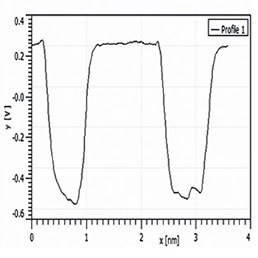
Внизу – СЭМ изображение специализированного проводящего зондового датчика компании MikroMasch. Одномерные сечения распределений поверхностного потенциала Φ измерены вдоль направлений, показанных стрелками.
О высоких значениях чувствительности и пространственного разрешения однопроходного КЗСМ-ФМ свидетельствуют изображения самосборки F14H20 на графитовой подложке (см. Рис. 5). В отличие от других подложек (Si, слюда), в адсорбатах F14H20 на графите первые слои молекулы ориентированы параллельно подложке и образуют ламеллярные структуры шириной 6–8 нм. В этом же направлении преимущественно ориентируются и молекулярные диполи этих слоев. Поэтому регистрируемый поверхностный потенциал для таких структур должен быть меньше, чем для самосборки F14H20 на кремниевой подложке. На крупномасштабных изображениях рельефа показаны несколько плоских ламелярных пластинок с большим количеством капель между ними. На каплях наблюдается небольшое отрицательное падение поверхностного потенциала (около –200 мВ), а на участках, занятых ламелями, и особенно в областях, не покрытых фторалканом, потенциал положителен. Такое поведение потенциала согласуется с предположением об ориентации молекулярных диполей параллельно плоскости подложки. Высокое разрешение по высоте и по поверхностному потенциалу позволило получить изображения (область сканирования – 80×80 нм), на которых внутри ламелярных структур видны изменения рельефа с 300 пм перепадом высот и потенциала в диапазоне 10–20 мВ. На этих снимках отчетливо видна периодическая структура с периодом 6 нм. Судя по ширине темных полос, достигнутое латеральное разрешение составляет несколько нанометров. Это объект представляет интерес для дальнейшего экспериментального и теоретического исследования [14].




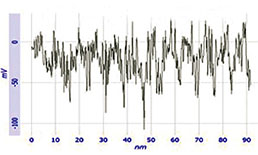
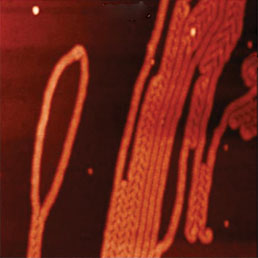
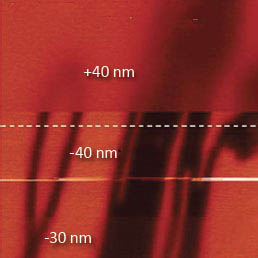
Для сравнения однопроходной КЗСМ-ФМ и двухпроходной методики были получены изображения самосборки F14H20 на подложке из слюды (см. Рис. 6). Сначала участок образца сканировался с помощью однопроходной КЗСМ-ФМ, а затем проводился второй проход при положительном (+40 нм) и отрицательном (–30 нм, –40 нм) смещениях зондового датчика по вертикали от исходного среднего положения. Амплитуда колебаний зонда составляла 50 нм. Контраст по поверхностному потенциалу Φ оказался очень низким при смещении +40 нм, он существенно возрос после смещения -40 нм (при дальнейшем увеличении смещения до 50 нм на изображении появляются искажения типа светлой полосы в центре профиля поверхностного потенциала, пример которого можно видеть на Рис. 6). Скачок поверхностного потенциала Φ при переходе от участков с самосборками F14H20 к открытой поверхности подложки составляет около –1.4 В для КЗСМ-ФМ и лишь –0.8 В для двухпроходной методики при смещении –40 нм. Сравнение значений поверхностного потенциала, полученных по однопроходной и по двухпроходной методикам, показывает предпочтительность первой из них для измерений подобного рода. Следует заметить, что для специализированных исследований электрических свойств может представлять определенный интерес комбинация градиентно-силовых методов с возможностью отрицательного смещения зондового датчика от среднего уровня. В настоящее время эту комбинацию можно реализовать только на сканирующих зондовых микроскопах компании НТ-МДТ СИ.
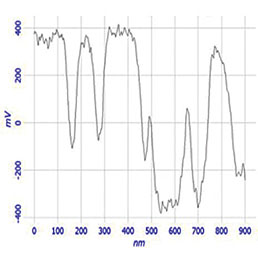

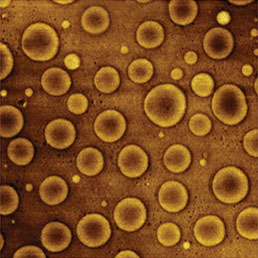
Как указывалось ранее, АСМ методики измерения электрических характеристик могут использоваться для изучения широкого спектра материалов, поскольку они лишены связанных с твердостью образца недостатков, ограничивающих применение методов локального измерения наномеханических свойств. Это демонстрируется измерениями структуры SRAM, изображения двух участков которой показаны на Рис. 7. Поверхностный потенциал полупроводниковых структур зависит от типа и концентрации легирующей примеси в точке измерения. Поэтому распределения высоты и поверхностного потенциала в этом случае могут заметно различаться. Изображения поверхностного потенциала Φ этих полупроводниковых структур весьма отличны от изображений поверхностного рельефа. Несколько неожиданным оказался тот факт, что изображения поверхностного потенциала структуры SRAM высокой степени интеграции и других полупроводниковых структур имели большую стабильность при использовании КЗСМ-АМ. Это подчеркивает необходимость надлежащей организации КЗСМ измерений в зависимости от типа образца, включая выбор метода измерений и типа зондового датчика. Для повышения отношения сигнал-шум при измерении локальных электрических характеристик рекомендуется применять зонды с большим радиусом кривизны острия. Такие зонды к тому же менее подвержены износу и прекрасно подходят для исследований, в которых не требуется высокое пространственное разрешение.




Еще один пример твердого материала, который можно эффективно исследовать с помощью КЗСМ, – припой из сплава висмута и олова, BiSn (см. Рис. 8). Образец для АСМ в виде плоской пластинки из этого сплава легкоплавких металлов можно приготовить, расплавив заготовку, зажатую между двумя плоскими поверхностями. Изображения рельефа поверхности, фазового контраста и поверхностного потенциала Φ такого образца показывают, что он имеет довольно гладкую поверхность ступенчатой структуры с участками высотой 10–20 нм. На изображении фазового контраста хорошо выделяются границы участков, тогда как изображение поверхностного потенциала Φ представляет совершенно другую картину, которая не коррелирует с изображением рельефа. Перепады поверхностного потенциала лежат в пределах 200 мВ, что близко к разности работ выхода Bi и Sn. Четкость двухуровневой картины поверхностного потенциала образца из сплава BiSn снижается неравномерным окислением поверхности, которому из двух компонентов сплава особенно подвержено олово. Этот фактор ухудшает резкость карты химического состава образца [14].

Следует отметить, что КЗСМ отличается от традиционных методик АСМ в том отношении, что она напрямую дает значение измеряемой характеристики образца. Например, в случае металлов поверхностный потенциал пропорционален локальной работе выхода, а в случае молекулярных систем с диполями он связан с моментами и ориентацией диполей. Кельвин-зондовая силовая микроскопия применяется также для изучения распределения свободных зарядов и их поведения при различных динамических воздействиях. Вместе с тем не следует переоценивать точность КЗСМ, особенно в отношении измерений, проводимых в обычных условиях. Неконтролируемое загрязнение образца или зонда может существенно уменьшить достоверность абсолютных значений поверхностного потенциала, полученных при таких измерениях. Следовательно, различия поверхностных потенциалов, измеренные в различных точках одного сканируемого участка, являются более надежными, чем абсолютные значения поверхностного потенциала.
ИЗМЕРЕНИЕ ЛОКАЛЬНЫХ ДИЭЛЕКТРИЧЕСКИХ ХАРАКТЕРИСТИК
Диэлектрическая спектроскопия широко используется для характеризации материалов, главным образом, с использованием макроскопических образцов. Она позволяет проводить измерения диэлектрических свойств в широком диапазоне частот и температур. Продвижение ее методик в область микро- и наномасштабов весьма актуально, и в этом направлении уже сделаны первые шаги. Как видно из уравнения (1), 2ωelec гармоника электростатической силы связана с производной dC/dZ, которая определяется локальными диэлектрическими свойствами образца. Эта зависимость легла в основу методики, реализованной в недавней работе [15]. В ней использовалась бесконтактная АСМ пленки поливинилацетата на проводящей подложке. В цепи обратной связи при ЧМ-АСМ измерении рельефа поверхности использовался контроллер с фазовой автоподстройкой частоты. Электростатическое взаимодействие индуцировалось переменным напряжением низкой частоты ωelec.
Локальная диэлектрическая проницаемость определялась по значениям амплитуды и фазы гармоники сигнала с частотой 2ωelec. Частотные зависимости действительной и мнимой частей сигнала V2ωelec сходны с диэлектрическими кривыми для макроскопических образцов, правда с температурным сдвигом на несколько градусов. Результаты измерений локальных диэлектрических характеристик при разных температурах также демонстрируют подобие частотных зависимостей с результатами измерений макроскопических аналогов. Другой пример АСМ исследования диэлектрического отклика – изучение поведения при разных температурах образца с тонкой пленкой, изготовленной из смеси PS и PVAC, [16]. В этой работе было показано, что участки PVAC легко обнаружить по хорошему фазовому контрасту, который наблюдается вблизи температуры стеклования этого полимера. При этом контраст матрицы, состоящей, по-видимому, преимущественно из PS, не изменяется, поскольку температура стеклования PS значительно выше.

Рельеф
Амп. Cosθ
RS-PVAC Map
RS-PS Map
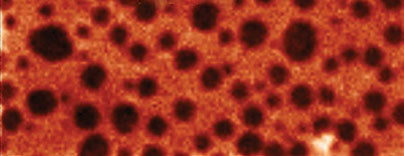
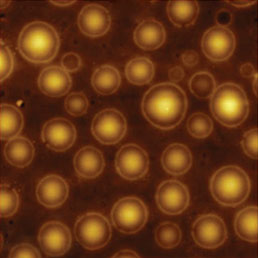
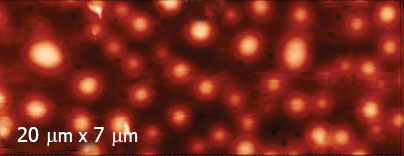
Следует отметить, что в упомянутых работах измерения проводились в условиях сверхвысокого вакуума бесконтактным методом. Для своих исследований однопроходных методик мы взяли образец из того же материала (смесь PS/PVAC), но для измерений использовали обычные (комнатные) условия. Изображения, типичные для тонких пленок из этого материала на подложке с проводящим ITO покрытием, показаны в левой части Рис. 9. Для морфологии пленки характерны сферические домены, внедренные в матрицу, что вполне согласуется с несмешиваемостью компонентов этой смеси, что приводит к их разделению. Поверхностный потенциал Φ доменов заметно (на ~200 мВ) превосходит потенциал матрицы, что можно объяснить большой разностью дипольных моментов молекул компонентов смеси (0.3 Д для PS и 2.1 Д для PVAC). Для диэлектрических измерений использовалась схема, показанная на Рис. 1, второй СД которой был настроен на частоту 2ωelec. В экспериментах с ФМ для ωelec удобно выбирать значение, лежащее в диапазоне 3-5 кГц. В большинстве диэлектрических измерений нами регистрировались амплитуда и фаза сигнала cosθ на частоте 2ωelec (для образца пленки PS/PVAC показано изображение амплитуды). Анализ этих изображений, существенно отличающихся от карты распределения поверхностного потенциала Φ, может оказаться весьма непростым. На первый взгляд кажется, что такой профиль есть просто инверсия изображения рельефа поверхности пленки.
Однако, как показывают исследования по морфологии пленок PS/PVAC при разных температурах в присутствии паров метанола [14] и измерения диэлектрических характеристик [16], в доменах преимущественно концентрируется PVAC, а матрица состоит, главным образом, из PS. В пользу этой модели говорят и данные по комбинационному рассеянию. Наиболее интенсивные полосы в рамановских спектрах PS (~1018 cm-1) и PVAC (~2959 cm-1) заметно различаются по частоте. Поэтому их целесообразно использовать для идентификации компонентов смеси. На рисунке показан рельеф участка пленки PS/PVAC и для сравнения там же приведены карты распределения интенсивности для основных полос полимеров PVAC и PS. Эти данные не оставляют сомнения в том, что домены состоят из PVAC, а матрица – из PS.
При отжиге пленки PS/PVAC при температуре выше температуры стеклования PVAC (~40 °C), но ниже температуры стеклования PS (~100 °C), происходит изменение морфологии пленки, которое, скорее всего, связано с перетеканием молекул PVAC из выступающих над поверхностью матрицы доменов в прилегающие к ним области. В результате между доменами образуются выступающие участки из этих молекул PVAC. Распределение поверхностного потенциала Φ также свидетельствует в пользу того, что эти выступающие участки имеют тот же химический состав, что и домены. Контраст профиля по диэлектрическому отклику заметно сильнее, чем у профилей по другим параметрам, и позволяет выявить более тонкие детали в областях сферических впадин. Как и на Рис. 9, распределение амплитуды 2ωelec гармоники косинуса фазы (cosθ) напоминает инверсию изображения рельефа.


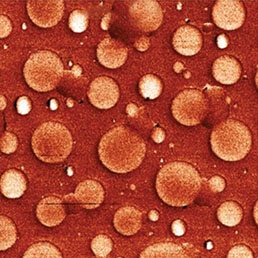
Как и в случае поверхностного потенциала, для регистрации диэлектрического отклика можно использовать различные схемы измерений. На Рис. 11. для сравнения приведены изображения, относящиеся к локальной диэлектрической проницаемости отожженных пленок PS/PVAC. ФМ измерения амплитуды косинуса фазы проводились на частоте 2ωelec=6 кГц.
АМ измерения производной dC/dZ также проводились на нерезонансной частоте электростатического возбуждения 2ωelec=6 кГц , а также на частоте второй моды колебаний кантилевера (2ωelec=405 кГц). Такой метод механического резонанса позволил заметно повысить отношение сигнал-шум, и для него контраст изображений оказался лучше, чем у двух других схем измерения локального диэлектрического отклика.

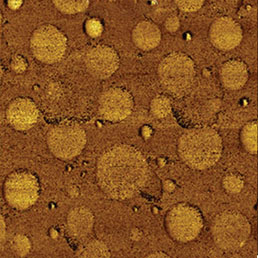
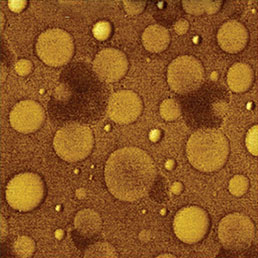
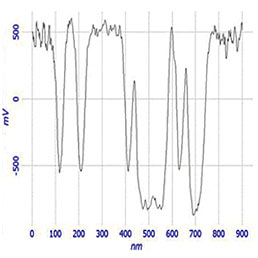
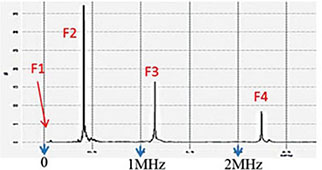
Следующий пример относится к самосборке частично фторированных алканов на подложке из слюды (Рис. 12). Алканы формируют систему полос, укладка которых происходит по эпитаксиальному механизму. Профиль поверхностного потенциала этого образца имеет отрицательный контраст, что указывает на вертикальную упаковку фторалкановых цепей. На профиле видны два выступающих нанокристалла, где потенциал не имеет отрицательных значений, что указывает на поперечную ориентацию молекул. В нашем исследовании профили локального диэлектрического отклика были измерены на разных частотах возбуждения. dC/dZ и cosθ отклики были измерены на нерезонансной низкой частоте 2ωelec=8 кГц. Для измерений на высоких частотах использовались две резонансные частоты кантилевера, соответствующие второй моде (406 кГц) и третьей моде (1.14 МГц). Эти частоты выбирались по АЧХ зондового датчика, также показанной на рисунке. Электростатическое возбуждение производилось на половинах второй и третьей изгибных мод, чтобы усилить отклик dC/dZ на частоте 2ωelec за счет корреляции с резонансами кантилевера. Как видно из полученных результатов, на низкой частоте (8 кГц) контраст сигнала косинуса фазы лучше, чем контраст амплитуды dC/dZ. Заметно различаются изображения фазы dC/dZ, снятые на разных частотах (8 кГц, 406 кГц и 1.14 МГц), что указывает на влияние динамики молекул фторалканов на регистрируемый диэлектрический отклик материала. Согласно данным диэлектрической спектроскопии по аналогичным материалам, во фторалканах наблюдается сильная β-релаксация, обусловленная вращением группы -(CF2)n- [17].
Рельеф










По сравнению с поверхностным потенциалом, который можно измерить непосредственно с помощью КЗСМ, в случае диэлектрического отклика количественный анализ оказывается заметно сложнее. Локальная емкость тонкой пленки зависит от ее толщины и локальной диэлектрической проницаемости [18]. Поэтому анализ изображений, связанных с диэлектрическим откликом, должен учитывать рельеф образца. Другая проблема связана с приведенными выше методами регистрации диэлектрического отклика. Высококонтрастные изображения можно получить, проведя измерения на частоте, равной частоте второй изгибной моды. Однако их количественная интерпретация осложняется усилением сигнала за счет высокой добротности кантилевера вблизи резонанса. Более прост анализ амплитуды и фазы сигнала cos2ωelec. Теоретическая модель динамики зондового датчика при использовании колебательного метода АСМ дает связь косинуса фазы сигнала и силы возбуждения колебаний кантилевера (уравнение 2.2). Это уравнение можно использовать и в случае электростатического взаимодействия между зондом и образцом, причем возникающий в этой модели интеграл представляется в аналитической форме [19]. В результате получается следующее соотношение между амплитудой косинуса фазы (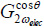 ), емкостью контакта между зондом и образцом [18], характеристиками зондового датчика и отношением толщины образца к его проницаемости:
), емкостью контакта между зондом и образцом [18], характеристиками зондового датчика и отношением толщины образца к его проницаемости:
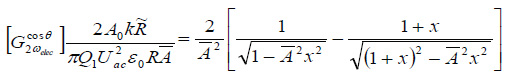
где ε0 – диэлектрическая постоянная вакуума, εr - относительная диэлектрическая проницаемость пленки; Q1 – добротность, h - толщина пленки, Zc – расстояние между зондом и образцом; θ0 – угол конусности зонда, R - эффективный радиус кривизны острия зонда; 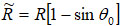 , A и A0 – амплитуды рабочих и свободных колебаний
, A и A0 – амплитуды рабочих и свободных колебаний
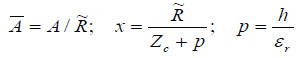
По этому соотношению можно определить величину проницаемости, если известны значения косинуса фазы, емкости и параметров зондового датчика. Эти формулы были положены нами в основу программы на платформе LabVIEW, с помощью которой были рассчитаны данные по двум полимерным пленкам [18].


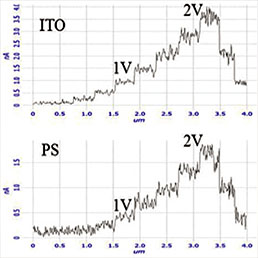
Проверка количественных диэлектрических измерений проводилась на тонких однородных пленках полимеров PS и PVAC, которые были приготовлены на стеклянных ITO подложках центрифугированием из раствора чистых полимеров. На этих пленках с помощью остро заточенной деревянной палочки были нанесены царапины на всю толщину, по которым можно было определить толщины пленок. Морфология участка пленки PS на ITO подложке показана на Рис. 13. Одновременно с рельефом регистрировался отклик косинуса фазы полимерной пленки при разных значениях возбуждающего напряжения. Как и ожидалось, амплитуда косинуса фазы квадратично зависит от приложенного напряжения. Для расчетов диэлектрической проницаемости использовались данные, полученные при амплитуде возбуждающего напряжения, равной 1 В (ωelec=4 кГц) с помощью зондов, имевших разные значения R радиуса кривизны острия. Сводка результатов вычислений представлена в Табл. 1. Из нее следует, что отношение проницаемостей PVAC и PS равно ~1.4, а значения этих параметров близки к величинам, найденным в экспериментах с макроскопическими образцами. В настоящее время ведутся работы по изучению температурной и частотной зависимостей локальных диэлектрических характеристик рассмотренных здесь полимеров и других объектов.
| Зонд, R=15 нм | R=30 нм | |||||
| Амплитуда | 19 нм | 18 нм | 48 нм | 19 нм | 38 нм | 76 нм |
| ε (PS) | 1,13 | 1,33 | 1,71 | 1,65 | 1,67 | 1,68 |
| ε (PVAC) | 1,80 | 1,90 | 2,18 | 2,36 | 2,25 | 2,30 |
| εPS/εPVAC | 1,59 | 1,43 | 1,27 | 1,43 | 1,35 | 1,37 |
ЗАКЛЮЧЕНИЕ
Разработка многочастотных методик электрических измерений с помощью АСМ, а также новых измерительных схем, позволяет значительно повысить чувствительность и разрешение КЗСМ и измерений локальных диэлектрических характеристик. Как показали исследования, проведенные на широком спектре материалов, эта модификация АСМ улучшает качество картирования состава многокомпонентных образцов. В дополнение к картированию растущий интерес представляют количественные измерения поверхностного потенциала и диэлектрической проницаемости. Представлен новый подход к определению значений проницаемости тонких полимерных пленок по АСМ измерениям. Впрочем, этот метод требует более детального изучения для приложений с более сложными материалами. Для дальнейшего прогресса в области измерения локальных диэлектрических характеристик необходимо расширить температурный и частотный диапазоны применения методик с электростатическим возбуждением.
ЛИТЕРАТУРА
[1] S. Belikov, and S. Magonov “Classification of Dynamic Atomic Force Microscopy Control Modes Based on Asymptotic Nonlinear Mechanics” Proceedings American Control Society, St. Louis, 979-985, 2009.
[2] Y. Martin, D. A. Abraham, and H. K. Wickramasinghe “High-resolution capacitance measurement and potentiometry by force microscopy” Appl. Phys. Lett. 1988, 52, 1103–10005.
[3] K. Kobayashi, H. Yamada, K. Matsushige, “Dopant profiling on semiconducting sample by scanning capacitance force microscopy” Appl. Phys. Lett. 2002, 81, 2629.
[4] V. B. Elings, and J. A. Gurley “Scanning probe microscope using stored data for vertical probe positioning” US Patent 5,308,974, 1994.
[5] J. Alexander, S. Magonov, and M. Moeller “Topography and surface potential in Kelvin forcemicroscopy of perfluoroalkyl alkanes self-assemblies” J. Vac. Sci. Technol. B 2009, 27, 903–911.
[6] S. Magonov, and J. Alexander “Single-pass Kelvin force microscopy and dC/dZ measurements in the intermittent contact: applications to polymer materials” Beilstein J. Nanotechnol.2011, 2, 15-27.
[7] U. Zerweck, CH. Loppacher, T. Otto, S. Grafstroem, and L. M. Eng “Accuracy and resolution limits of Kelvin probe force microscopy” Phys. Rev. B 2005, 71, 125424.
[8] F. Krok, K. Sajewicz, J. Konior, M. Goryl, P. Piatkowski, and M. Szymonski “Lateral resolution and potential sensitivity in Kelvin probe force microscopy: Towards understanding of the sub-nanometer resolution” Phys. Rev. B 2008, 77, 235427–235429.
[9] J. Colchero, A. Gil, and A. M. Baro “Resolution enhancement and improved data interpretation in electrostatic force microscopy” Phys. Rev. B 2001, 64, 245403.
[10] F. Giessibl “Forces and frequency shifts in atomic-resolution dynamic-force microscopy” Phys. Rev. B1997, 56, 16010-16015.
[11] S. Magonov, J. Alexander, S.-H. Jeoung, and N. Kotov “High-resolution imaging of molecular and nanoparticles self-assemblies with Kelvin force microscopy” J. Nanosci. Nanotechnol.2010, 10, 1-5.
[12] A. Mourran, A.; Tartsch, B.; Gallyamov, M.; Magonov, S.; Lambreva, D.; Ostrovskii, B. I.; Dolbnya, I. P.; de Jeu, W. H.; M. Moeller, “Self-assembly of the perfluoroalkyl-alkane F14H20 in ultrathin films”. Langmuir2005, 21, 2308–2316.
[13] A. El Abed, M-C. Faure, E. Pouzet, and O. Abilon “Experimental evidence for an original two-dimensional phase structure: An antiparallel semifluorinated monolayer at the air-water interface” Phys. Rev. E 2002, 5, 051603–051604.
[14] S. Magonov, J. Alexander, and S. Wu “Advancing characterization of materials with Atomic Force Microscopy – based electric techniques. In Scanning Probe Microscopy of Functional Materials: NanoscaleImaging and Spectroscopy; Kalinin, S. V.; Gruverman, A., Eds.; Springer: Berlin, Germany, 2010; pp 233–300.
[15] P. S. Crider, M. R. Majewski, J. Zhang, H. Oukris, and N. E. Israeloff “Local dielectric spectroscopy of near-surface glassy polymer dynamics” 2008, 128, 044908-5.
[16] C. Riedel,R. Arinero, Ph. Tordjeman,G. Lévêque, G. A. Schwartz, A. Alegria, and J. Colmenero“Nanodielectric
mapping of a model polystyrene-poly(vinyl acetate) blend by electrostatic force microscopy”Phys. Rev. E2010, 81, 010801-010804.
[17] K. Araki, K. Satoh, and S. Kondo “Dielectric behavior of semifluorinated n-alkane (F(CF2)n(CH2)mH)” Mol. Cryst. Liq. Cryst.1996, 281, 123-134.
[18] G. Gomila, J. Toset, and L. Fumagali, “Nanoscale capacitance microscopy of thin dielectric films” J. Appl. Phys.2008, 104, pp. 024315 1-8.
[19]. S. Belikov, J. Alexander, S. Magonov, and I. Yermolenko “Atomic force microscopy control system for electrostatic measurements based on mechanical and electrical modulation” Amer. Control Conf.2012, 3238-3233.