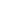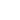2.1.1 Закон Гука
Кантилевер – это наиболее распространненый датчик силового взаимодействия в атомно-силовой микроскопии. Любую информацию о поверхности атомно-силовой микроскоп получает благодаря механическим отклонениям балки кантилевера, которые регистрируются оптической системой. Для бесконтактной микроскопии часто используют резонаторы камертонного типа вместо кантилеверов. В таком сенсоре следят за изменением резонансной частоты при появлении силового взаимодействия зонда с поверхностью.
Обычно кантилевер представляет собой балку в виде прямоугольного параллелепипеда (рис. 1a), имеющего длину
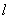, толщину
(
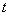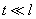) и ширину
(
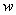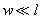) или в виде двух балок, соединенных под некоторым углом (рис. 1б), с зондом (острием) длиной
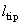на одном из ее концов. Далее подробно рассмотрим прямоугольный кантилевер. Геометрические размеры, характеризующие его, показаны на рис. 1а. С поверхностью взаимодействует острие зонда. Будем считать, что именно к его вершине приложена сосредоточенная сила, действующая со стороны исследуемого образца.
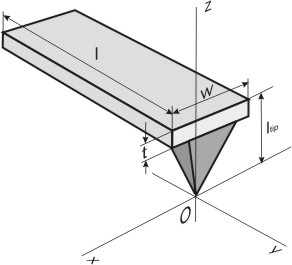
Рис. 1а. Прямоугольный кантилевер с зондом.
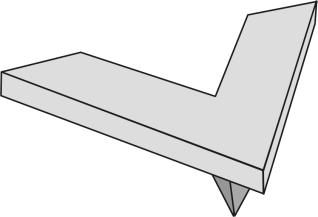
Рис. 1б. Треугольный кантилевер с зондом.
Сила, действующая на зонд, зачастую имеет не только вертикальную составляющую, но и компоненты, лежащие в горизонтальной плоскости. Поэтому острие кантилевера может отклоняться не только вдоль оси
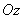-но в двух других направлениях:
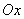и
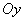(см. рис. 1а). Вертикальную составляющую
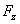назовем нормальной силой, поперечную
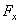и продольную
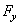– латеральными силами.
Так как в АСМ о силе воздействия образца на кантилевер судят по деформации последнего, то для определения силы, необходимо знать жесткость деформаций кантилевера в различных направлениях. Считаем, что вектор отклонения острия кантилевера
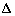(имеющий компоненты
,
,
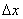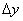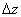) связан с приложенной к зонду силой
линейно, т.е. по закону Гука [1]:
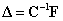
(1)
"Коэффициентом" пропорциональности служит тензор второго ранга
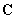который назовем тензором обратной жесткости. Эта величина содержит всю информацию об упругих свойствах кантилевера.
Чтобы найти компоненты тензора
,
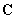необходимо решить задачи о статических деформациях кантилевера под действием сил, направленных по разным осям. Для наглядности запишем формулу (1) в матричном виде:
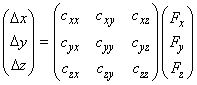
(2)
Заметим, что оптическая система регистрирует не отклонение острия кантилевера, а наклон верхней поверхности кантилевера вблизи его свободного конца. Непосредственно измеряются два угла: отклонение нормали от вертикали в плоскости
(угол
) и в ортогональном направлении – плоскости
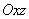(угол
).
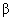Для удобства расчетов можно вместо (2) записать матричное соотношение, связывающее углы
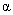и
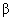непосредственно с компонентами силы
.
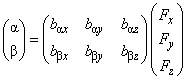
(3)
Однако введенная матрица в отличие от тензора
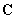не содержит полной информации об упругих свойствах кантилевера.
Выводы.
- Информацию об образце в АСМ можно получить только из деформации кантилевера. Оптическая система позволяет измерять два угла, задающие отклонение верхней плоскости кантилевера.
- Чтобы по отклонению зонда определить силу, действующую на кантилевер, необходимо знать его упругие свойства, которые описываются тензором второго ранга обратной жесткости кантилевера.
- Связь деформации и силы моделируется линейным законом Гука тензорного вида.
Литература.
- Handbook of Micro/Nanotribology / Ed. by Bhushan Bharat. - 2d ed. - Boca Raton etc.: CRC press, 1999. – 859 c.