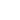2.2.2.3 Точная постановка задачи Герца и ее решение в общем виде
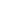
Пусть два твердых тела соприкасаются друг с другом в точке (рис. 1). Необходимо принять следующие упрощающие предположения [1]:
- Тела заполнены однородными изотропными линейно упругими средами, характеризующимися модулями Юнга
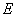 ,
,
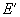 и коэффициентами Пуассона
и коэффициентами Пуассона
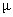 ,
,
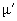 .
. - Кривизна поверхностей мало влияет на напряженно-деформированное состояние.
- Граничные поверхности заменяются эллиптическими параболоидами.
- Точка контакта – не особая, область контакта односвязная и ее граница – эллипс.
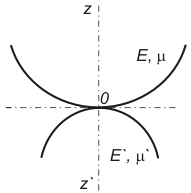
Рис. 1. Соприкосновение двух тел до деформации.
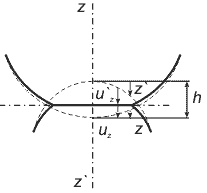
Рис. 2. Пунктиром изображены поверхности до деформации, а сплошной линией – поверхности сдавленных тел. Буквы
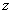 и
и
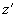 обозначают длины, определяемые равенствами (1) и (2).
обозначают длины, определяемые равенствами (1) и (2).
Уравнение поверхности вблизи точки касания:
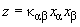
(1)
где по дважды повторяющимся индексам
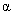 ,
,
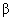 – суммирование. Тензор
– суммирование. Тензор
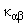 характеризует кривизну поверхности, его главные значения –
характеризует кривизну поверхности, его главные значения –
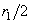 и
и
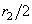 (здесь
(здесь
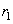 ,
,
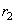 – главные радиусы кривизны контактирующих поверхностей в точке O).
– главные радиусы кривизны контактирующих поверхностей в точке O).
Аналогично для второго тела:
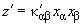
(2)
Предположим, что тела сдавливаются некоторой силой
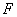 , в результате чего они деформируются и сближаются на некоторое малое расстояние
, в результате чего они деформируются и сближаются на некоторое малое расстояние
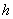 (рис. 2). Теперь областью соприкосновения будет не точка, а участок поверхности площадью
(рис. 2). Теперь областью соприкосновения будет не точка, а участок поверхности площадью
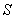 (
(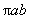 для эллипса). Пусть
для эллипса). Пусть
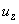 и
и
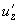 компоненты (соответственно по осям
компоненты (соответственно по осям
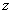 и
и
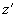 векторов смещения точек поверхностей обоих тел при сдавливании (рис. 2).
векторов смещения точек поверхностей обоих тел при сдавливании (рис. 2).
Из рисунка видно, что в точках области соприкосновения имеет место равенство:
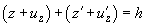
(3)
или
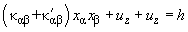
(4)
В точках, где поверхности не соприкасаются, выполняется
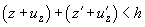
(5)
Выберем направления осей
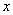 и
и
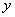 таким образом, чтобы тензор
таким образом, чтобы тензор
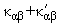 был приведен к главным осям. Обозначая через
был приведен к главным осям. Обозначая через
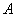 и
и
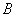 главные значения этого тензора, перепишем (4):
главные значения этого тензора, перепишем (4):
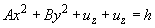
(6)
Величины
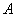 и
и
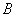 связаны с радиусами кривизны
связаны с радиусами кривизны
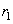 ,
,
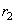 и
и
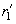 ,
,
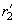 обеих поверхностей следующими формулами, которые приведем без вывода:
обеих поверхностей следующими формулами, которые приведем без вывода:
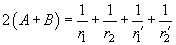
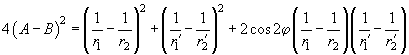
(7)
где
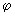 – угол между теми нормальными сечениями поверхностей, в которых радиусы кривизны –
– угол между теми нормальными сечениями поверхностей, в которых радиусы кривизны –
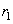 и
и
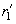 . Знаки радиусов кривизны положительны, если соответствующие центры кривизны расположены внутри соответствующего тела, и отрицательны – в обратном случае.
. Знаки радиусов кривизны положительны, если соответствующие центры кривизны расположены внутри соответствующего тела, и отрицательны – в обратном случае.
Обозначим через
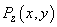 давление между сдавленными телами в точках их соприкосновения. Вне области соприкосновения, очевидно,
давление между сдавленными телами в точках их соприкосновения. Вне области соприкосновения, очевидно,
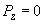 . Смещение
. Смещение
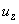 под влиянием нормальных сил
под влиянием нормальных сил
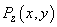 определяется выражением (поверхности считаем плоскими):
определяется выражением (поверхности считаем плоскими):
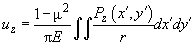
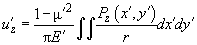
(8)
Заметим, что из (8) следует, что отношение
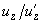 постоянно и равно:
постоянно и равно:
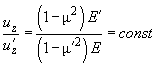
(9)
Соотношения (7) и (9) непосредственно определяют распределение деформации
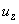 и
и
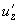 по области соприкосновения. Подставим выражения (8) в (7):
по области соприкосновения. Подставим выражения (8) в (7):
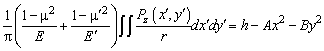
(10)
Это интегральное уравнение определяет распределение давления
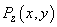 по области соприкосновения. Решение его находится по аналогии с теорией потенциала.
по области соприкосновения. Решение его находится по аналогии с теорией потенциала.
Поэтому придется рассмотреть задачу из теории потенциала..
Пусть по объему трехосного эллипсоида
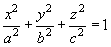
(11)
равномерно распределен заряд (с объёмной плотностью
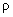 ). Тогда потенциал поля внутри эллипсоида определяется выражением:
). Тогда потенциал поля внутри эллипсоида определяется выражением:
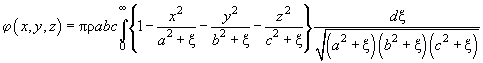
(12)
В предельном случае предельно уплощенного эллипсоида (в направлении оси
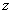 ), когда
), когда
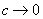 :
:
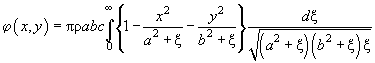
(13)
(координаты
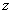 внутри эллипсоида полагаются равными нулю).
внутри эллипсоида полагаются равными нулю).
Потенциал можно записать и по-другому:
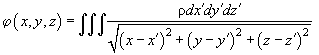
(14)
где интегрирование производится по объёму эллипса. Теперь перейдем к пределу
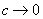 , при этом положим под корнем
, при этом положим под корнем
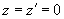 ; производя интегрирование по
; производя интегрирование по
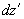 в пределах между
в пределах между
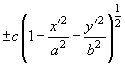 , получим:
, получим:
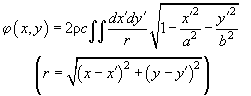
(15)
где интегрирование производится по площади внутри эллипса
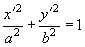 Приравнивая оба выражения для
Приравнивая оба выражения для
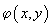 , получим:
, получим:
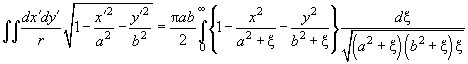
(16)
Сравним интегральное уравнение (16) с уравнением (10). Видим, что в их правых частях стоят квадратичные функции от
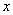 и
и
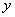 одинакового вида, а в левых – интегралы одинакового типа. Поэтому можно сразу сказать, что область соприкосновения тел (она же – область интегрирования в интеграле (10)) ограничена эллипсом вида:
одинакового вида, а в левых – интегралы одинакового типа. Поэтому можно сразу сказать, что область соприкосновения тел (она же – область интегрирования в интеграле (10)) ограничена эллипсом вида:
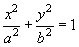
(17)
и что функция
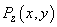 должна быть вида:
должна быть вида:
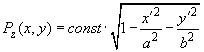
(18)
Выберем const таким образом, чтобы интеграл
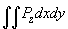 по области соприкосновения был равен силе
по области соприкосновения был равен силе
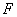 с которой сдавливаются тела. Получим:
с которой сдавливаются тела. Получим:
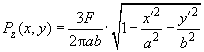
(19)
Эта формула определяет закон распределения давления по площади области соприкосновения. Заметим, что давление в центре в полтора раза превышает среднее давление
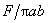 .
.
Подставим (19) в (10) и заменим получающийся интеграл его выражением согласно (16):
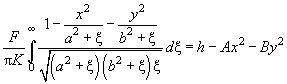
(20)
где
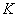 – эффективный модуль Юнга:
– эффективный модуль Юнга:
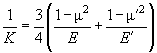
(21)
Приравняем коэффициенты при
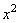 и
и
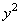 и свободные члены с обеих сторон:
и свободные члены с обеих сторон:
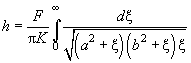
(22)
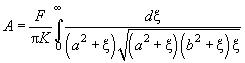
(23)
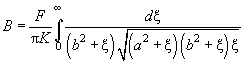
(24)
Уравнения (22), (23) определяют полуоси
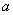 и
и
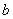 области соприкосновения при заданной силе
области соприкосновения при заданной силе
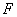 (
(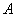 и
и
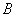 известные для данных тел величины). После этого с помощью соотношения (22) можно определить зависимость между силой
известные для данных тел величины). После этого с помощью соотношения (22) можно определить зависимость между силой
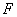 и вызываемым ею сближением тел
и вызываемым ею сближением тел
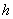 . Интегралы в правых частях уравнений эллиптические.
. Интегралы в правых частях уравнений эллиптические.
Применим полученные формулы к соприкосновению двух шаров с радиусами
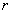 и
и
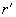 . В этом случае:
. В этом случае:
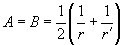
(25)
Из соображений симметрии ясно, что
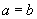 , т.е. областью соприкосновения является круг. Из (23), (24) получим для радиуса области соприкосновения:
, т.е. областью соприкосновения является круг. Из (23), (24) получим для радиуса области соприкосновения:
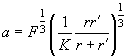
(26)
В данном случае
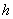 – это разность между суммой
– это разность между суммой
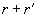 и расстоянием между центрами шаров. Из (18) получим соотношение между
и расстоянием между центрами шаров. Из (18) получим соотношение между
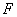 и
и
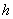 :
:
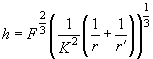
(27)
Итак,
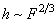 , соответственно,
, соответственно,
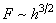 .
.
Зависимость вида
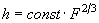 ,
,
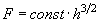 имеет место не только для шаров, но и для других тел конечных размеров. В этом легко убедиться из соображений подобия. Если провести замену
имеет место не только для шаров, но и для других тел конечных размеров. В этом легко убедиться из соображений подобия. Если провести замену
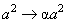 ,
,
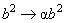 ,
,
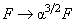 , где
, где
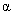 – произвольная постоянная, то уравнения (23), (24) останутся неизменными. В уравнении же (22) правая часть умножится на
– произвольная постоянная, то уравнения (23), (24) останутся неизменными. В уравнении же (22) правая часть умножится на
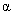 , и для того, чтобы оно оставалось неизменным, надо изменить
, и для того, чтобы оно оставалось неизменным, надо изменить
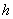 на
на
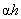 . Отсюда следует, что
. Отсюда следует, что
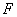 должно быть пропорционально
должно быть пропорционально
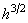 .
.
Выводы.
- Задача Герца позволяет определить параметры деформации в "точке" соприкосновения двух тел.
- При постановке задачи Герца используется модель сплошной упругой однородной среды и предположение малости деформаций.
- В месте "точечного" соприкосновения зонда с поверхностью образца образуется контактная площадка.
- Решение задачи Герца позволяет определить величину прогиба в зависимости от приложенной нагрузки. Величина прогиба
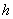 пропорциональна степени
пропорциональна степени
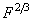 сдавливающей силы.
сдавливающей силы.
Литература.
- Ландау Л.Д., Лившиц Е.М. Теория упругости. – М.: Наука, 1987. – 246 с.