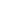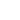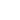Приложения
Приложение 1. Вычисление силы и градиента силы действующей на цилиндрический
ферромагнитный зонд в магнитном поле проводника.
Найдём силу и производную силы, действующую на цилиндрический ферромагнитный зонд радиуса
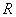 , длиной
, длиной
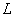 и намагниченностью
и намагниченностью
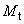 находящегося в магнитном поле проводника. Причём, вектор намагниченности
находящегося в магнитном поле проводника. Причём, вектор намагниченности
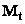 направлен под углом
направлен под углом
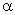 к нормали основания цилиндра по всему объёму (рис. 1).
к нормали основания цилиндра по всему объёму (рис. 1).
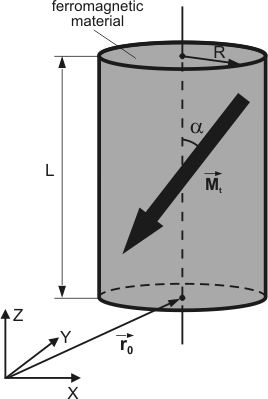
Рис. 1. Схематическое изображение цилиндрического зонда.
Вектор
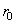 имеет координаты
имеет координаты
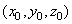 .
.
Согласно пункту 2.7.3 силу
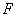 , действующую на магнитный кантилевер, и её производную
, действующую на магнитный кантилевер, и её производную
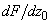 , можно вычислить, проинтегрировав по всему объёму ферромагнитного материала силу, действующую на элементарный объём. Для данной геометрии магнитного зонда и при условии, что магнитное поле вдоль оси Y равно нулю, сила и производная вдоль оси Z, в соответствии с формулами (1, 2) пункта 2.7.3 определяются через функцию
, можно вычислить, проинтегрировав по всему объёму ферромагнитного материала силу, действующую на элементарный объём. Для данной геометрии магнитного зонда и при условии, что магнитное поле вдоль оси Y равно нулю, сила и производная вдоль оси Z, в соответствии с формулами (1, 2) пункта 2.7.3 определяются через функцию
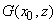 следующим образом
следующим образом
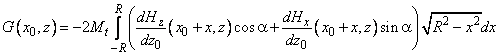
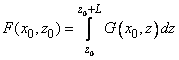
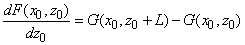
(1)
где аналитические зависимости производных магнитного поля
 определяются формулами (9,10) пункта 2.7.9.
определяются формулами (9,10) пункта 2.7.9.
Приложение 2. Вычисление силы и градиента силы действующей на сферический
ферромагнитный зонд в магнитном поле проводника.
Найдём силу и производную силы, действующую на сферический ферромагнитный зонд радиуса
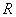 , и намагниченностью
, и намагниченностью
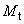 находящегося в магнитном поле проводника. Причём, вектор намагниченности
находящегося в магнитном поле проводника. Причём, вектор намагниченности
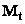 направлен под углом
направлен под углом
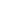
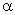 к оси Z по всему объёму (рис. 2).
к оси Z по всему объёму (рис. 2).
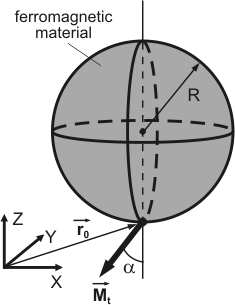
Рис. 2. Схематическое изображение сферического зонда.
Вектор
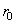 имеет координаты
имеет координаты
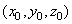 .
.
Согласно пункту 2.7.3 силу
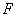 , действующую на магнитный кантилевер, и её производную
, действующую на магнитный кантилевер, и её производную
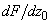 , можно вычислить, проинтегрировав по всему объёму ферромагнитного материала силу, действующую на элементарный объём. Для данной геометрии магнитного зонда и при условии, что магнитное поле вдоль оси Y равно нулю, сила и производная вдоль оси Z, в соответствии с формулами (1, 2) пункта 2.7.3 определяются выражениями
, можно вычислить, проинтегрировав по всему объёму ферромагнитного материала силу, действующую на элементарный объём. Для данной геометрии магнитного зонда и при условии, что магнитное поле вдоль оси Y равно нулю, сила и производная вдоль оси Z, в соответствии с формулами (1, 2) пункта 2.7.3 определяются выражениями

(2)
где
 и аналитические зависимости производных магнитного поля
и аналитические зависимости производных магнитного поля
 определяются формулами (9,10) пункта 2.7.9.
определяются формулами (9,10) пункта 2.7.9.
Приложение 3. Вычисление силы и градиента силы действующей на конический зонд,
покрытый ферромагнитной плёнкой в магнитном поле проводника.
Найдём силу и производную силы, действующую на конический зонд покрытый ферромагнитной плёнкой в магнитном поле проводника. Зонд имеет радиус
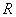 , длину
, длину
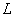 , углол раствора
, углол раствора
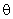 , покрыт ферромагнитной плёнкой толщиной
, покрыт ферромагнитной плёнкой толщиной
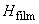 и намагниченностью
и намагниченностью
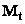 , направленной вдоль оси Z (рис. 3).
, направленной вдоль оси Z (рис. 3).
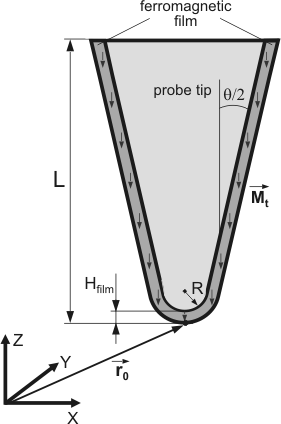
Рис. 3. Сечение конического зонда покрытого ферромагнитной плёнкой.
Вектор
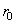 имеет координаты
имеет координаты
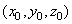 .
.
Согласно пункту 2.7.3 силу
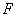 , действующую на магнитный кантилевер, и её производную
, действующую на магнитный кантилевер, и её производную
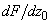 , можно вычислить, проинтегрировав по всему объёму ферромагнитного материала силу, действующую на элементарный объём. Для простоты выполнения поставленной задачи, разобьём интегрирование по объёму ферромагнитного материала на три этапа.
, можно вычислить, проинтегрировав по всему объёму ферромагнитного материала силу, действующую на элементарный объём. Для простоты выполнения поставленной задачи, разобьём интегрирование по объёму ферромагнитного материала на три этапа.
Первый этап – вычисляется сила и её производная, действующая на сферическую часть зонда. Для сферической части магнитного зонда при условии, что магнитное поле вдоль оси Y равно нулю, сила и производная вдоль оси Z, в соответствии с формулами (1, 2) пункта 2.7.3 определяются выражениями
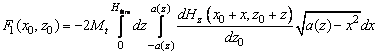
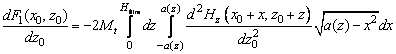
(3)
где
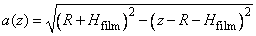 и аналитические зависимости производных магнитного поля
и аналитические зависимости производных магнитного поля
 определяются формулами (9,10) пункта 2.7.9.
определяются формулами (9,10) пункта 2.7.9.
Второй этап – вычисление силы и её производной, действующей на немагнитный внутренний конус, предполагая, что вектор намагниченности по всему объёму конуса не равен нулю, а совпадает с
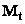 . Вычисление силы и её производной также выполняется в соответствии с формулами (1, 2) пункта 2.7.3, которые дают результат
. Вычисление силы и её производной также выполняется в соответствии с формулами (1, 2) пункта 2.7.3, которые дают результат

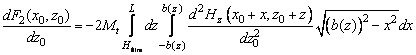
(4)
где
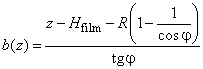 и
и
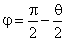 .
.
Третий этап – вычисление силы и её производной по всему объёму внешнего конуса, за исключением сферической части зонда и предполагая, что вектор намагниченности во всем объёме конуса совпадает с
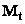 . В этом случае
. В этом случае
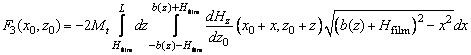
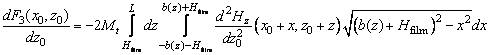
(5)
Соответственно, общая сила и её производная, действующая на зонд данного типа, определяются выражениями
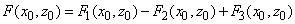
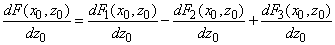
(6)
Приложение 4. Вычисление силы и градиента силы действующей на конический
ферромагнитный зонд в магнитном поле проводника.
Найдём силу и производную силы, действующую на конический ферромагнитный зонд в магнитном поле проводника. Зонд имеет радиус
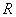 , длину
, длину
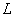 , углол раствора
, углол раствора
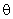 и намагниченность
и намагниченность
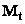 , направленную под углом
, направленную под углом
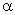 к оси Z (рис. 4).
к оси Z (рис. 4).
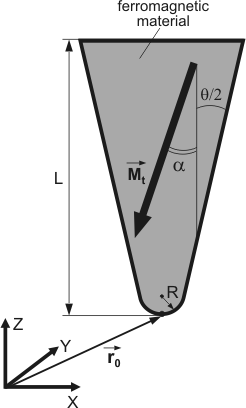
Рис. 4. Сечение конического ферромагнитного зонда.
Вектор
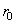 имеет координаты
имеет координаты
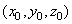 .
.
Согласно пункту 2.7.3 силу
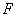 , действующую на магнитный кантилевер, и её производную
, действующую на магнитный кантилевер, и её производную
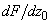 , можно вычислить, проинтегрировав по всему объёму ферромагнитного материала силу, действующую на элементарный объём. Для простоты выполнения поставленной задачи, разобьём интегрирование по объёму ферромагнитного материала на два этапа.
, можно вычислить, проинтегрировав по всему объёму ферромагнитного материала силу, действующую на элементарный объём. Для простоты выполнения поставленной задачи, разобьём интегрирование по объёму ферромагнитного материала на два этапа.
Первый этап – вычисляется сила и её производная, действующая на сферическую часть зонда. Для сферической части магнитного зонда при условии, что магнитное поле вдоль оси Y равно нулю, сила и производная вдоль оси Z, в соответствии с формулами (1, 2) пункта 2.7.3 определяются выражениями
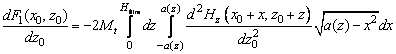
(7)
где
 ,
,
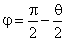 и аналитические зависимости производных магнитного поля определяются формулами (9,10) пункта 2.7.9.
и аналитические зависимости производных магнитного поля определяются формулами (9,10) пункта 2.7.9.
Второй этап – вычисление силы и её производной по всему объёму конуса, за исключением сферической части. Вычисление силы и её производной также выполняется в соответствии с формулами (1, 2) пункта 2.7.3, которые дают результат

(8)
где
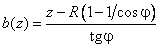 .
.
Соответственно, общая сила и её производная, действующая на зонд данного типа, определяются выражениями
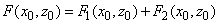
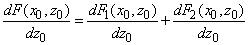
(9)