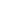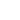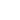2.1.6 Эффективная масса и собственная частота кантилевера
В АСМ помимо методик, основанных на измерении статического изгиба балки, существуют колебательные методики. Для их использования необходимо знать резонансную частоту кантилевера.
Вычислим резонансную частоту изотропного кантилевера массы
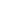
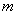в виде балки в форме параллелепипеда длиной
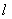, толщиной
(
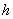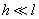) и шириной
(
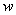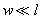) на свободный конец которого действует сосредоточенная вертикальная сила
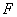(рис. 1).
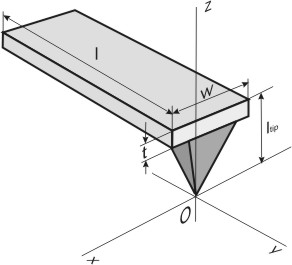
Рис. 1. Прямоугольный кантилевер с зондом.
Найдём кинетическую
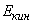и потенциальную
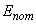энергию кантилевера. Рассмотрим элемент балки длиной
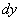находящийся на расстоянии
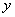от закреплённого конца. Кинетическая энергия такого элемента есть:
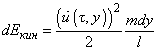
(1)
где
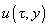– отклонение точек осевой линии балки на расстоянии
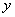от закреплённого конца в момент времени
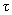. В соответствии с формулами (8), (9) пункта 2.1.2
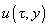выражается через отклонение свободного конца балки
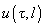следующим образом:
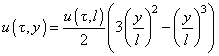
(2)
Тогда подставляя значение
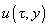в (1) и производя интегрирование по всей длине балки, получим, что
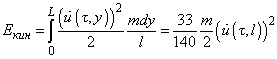
(3)
Потенциальная энергия вычисляется проще. Так как по условию только на свободный конец действует сосредоточенная сила F , то очевидно, что Enom равна работе, затраченной на перемещение конца балки на расстояние
:
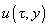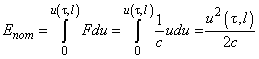
(4)
где
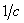– коэффициент нормальной жесткости, определяемый формулой (12) пункта 2.1.2.
Если считать, что колебания в системе происходят без диссипации полной энергии
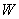то есть
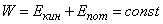, then, differentiating
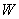тогда дифференцируя полную энергию по времени, получим уравнение движения свободного конца кантилевера
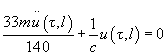
(5)
Следовательно, эффективная масса кантилевера равна
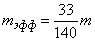
(6)
Таким образом, вычислив
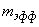и зная коэффициент жёсткости
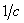определяемый формулой (12) пункта 2.1.2 получаем, что собственная частота колебаний кантилевера выражается через его параметры следующим образом
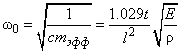
(7)
где
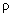– плотность кантилевера,
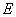– модуль Юнга. Как видно из (6),
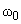обратно пропорциональна квадрату длины балки. Данный факт необходимо учитывать при выборе кантилевера. Резонансная частота собственных колебаний кантилевера должна быть максимально высокой, иначе в нём легко будут возбуждаться собственные колебания за счёт возвратно-поступательных перемещений зонда относительно образца при построчном сканировании поверхности или под действием внешних вибраций.
Выводы.
- Для использования колебательных методик АСМ необходимо знать частоту собственных колебаний и эффективную массу кантилевера.
- Эффективная масса
.
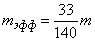- Собственная частота
.
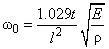