1.1.1 Функция состояния системы, уравнение Шредингера. Туннельный эффект

Представление о туннелировании частиц возникло почти одновременно с квантовой механикой. В классической механике для описания в какой-то момент времени системы материальных точек достаточно задать значение координат и компонент импульса каждой из материальных точек. В квантовой механике даже для одной частицы одновременное определение координат и соответствующей ей компоненты импульса принципиально невозможно из-за соотношения Гейзенберга. Наиболее полное описание системы в квантовой механике дается комплексной функцией состояния системы (волновой функцией). Функция состояния 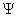, зависящая от времени и координат всех частиц системы, является решением волнового уравнения Шредингера. Физический смысл функции состояния системы определяется не самой 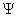, а . 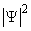Вероятность нахождения частиц в элементарном объеме dxdydz есть не что иное, как .

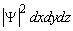При рассмотрении падения частиц на потенциальный барьер конечной ширины квантовая механика предсказывает неизвестный в классической физике эффект – прохождение частиц сквозь потенциальный барьер, даже если полная энергия частицы меньше высоты этого барьера.

Вычислим прозрачность потенциального барьера прямоугольной формы [1, 2]. Рассмотрим падение пучка электронов на потенциальный барьер прямоугольной формы, при котором потенциальная энергия частиц

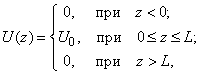
(1)

а полная энергия E меньше чем U₀ (рис. 1).

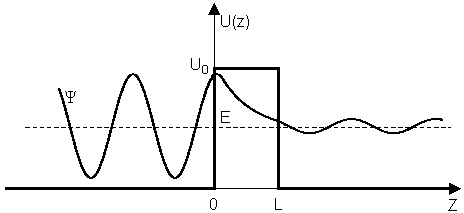
Рис. 1. Прямоугольный потенциальный барьер и волновая функция частицы .

Стационарные уравнения Шредингера имеют вид:

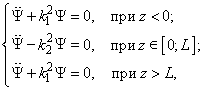
(2)

где 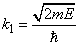, 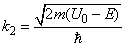– волновые вектора, 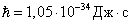– постоянная Планка. Решение волнового уравнения при ищем в виде суммы падающей и отражённой волны 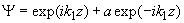, а решение при 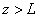– в виде прошедшей волны 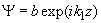. Решение в области потенциального барьера 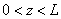есть 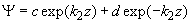. Постоянные коэффициенты a, b, c, d определяются из условия непрерывности волновой функци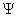и и 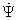в точках 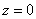и .

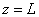В качестве коэффициента прозрачности барьера D естественно взять отношение плотности потока вероятности прошедших частиц к плотности потока вероятности частиц, падающих на барьер. В рассматриваемом случае, это отношение будет просто равно квадрату модуля волновой функции, оказавшейся за барьером, так как амплитуда падающей волны принята за единицу, а волновые вектора падающей и прошедшей волны совпадают

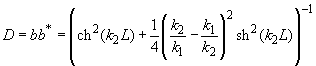
(3)

если 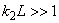, то как 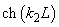так и 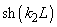можно приблизительно заменить на 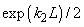и тогда выражение (3) примет вид

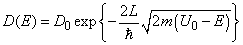
(4)

где

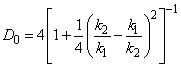
Таким образом, аналитическое вычисление коэффициента прохождения через потенциальный барьер прямоугольной формы является достаточно простой задачей. Однако, во многих квантово-механических задачах, необходимо вычислить коэффициент прохождения через барьер более сложной формы. В этом случае, общего аналитического решения вычисления коэффициента D не существует. Тем не менее, если параметры задачи удовлетворяют условиям квазиклассичности, то коэффициент прохождения через барьер может быть вычислен в общем виде (см. пункт 1.1.2).

Выводы.

В квантовой механике под туннельным эффектом подразумевается прохождение частиц сквозь потенциальный барьер, когда полная энергия частиц меньше высоты этого барьера.
Чтобы вычислить коэффициент прозрачности необходимо решить уравнения Шредингера системы с учётом условий сшивки волновой функции на границах барьера.
Коэффициент прозрачности прямоугольного барьера в случае, когда волновые векторы падающей и прошедшей волны совпадают экспоненциально убывает с увеличением ширины барьера.

Литература.

Д.В. Сивухин. Курс общей физики // М.: Наука, т.5, ч.1 1988.
Л.Л. Гольдин., Г.И. Новикова. Введение в квантовую физику // М.: Наука 1988.